| I work in the area of statistical mechanics. Recent research has been in microstructure of bone, hard core exclusion models, granular systems, polyelectrolytes and nonequilibrium statistical mechanics. |  |
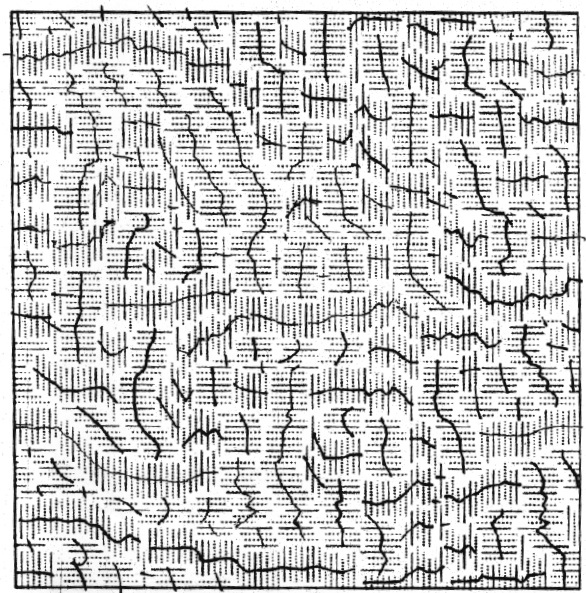
| Cortical bone, found in the central part of long bones like femur, is known to adapt to local mechanical stresses. This adaptation has been linked exclusively with Haversian remodelling involving bone resorption and formation of secondary osteons. Compared to primary/plexiform bone, the Haversian bone has lower stiffness, fatigue strength and fracture toughness, raising thequestion why nature prefers an adaptation that is detrimental to bone's primaryfunction of bearing mechanical stresses. In the goat femur, several microstructures may be seen when the length of the bone is traversed (see image below). We show that in the goat femur, Haversian remodelling occurs only at locations of high compressive stresses. At locations corresponding to high tensile stresses, a non-Haversian microstructure is observed. Compared with primary/plexiform bone, this microstructure's mineralisati on is significantly higher with a distinctly different spatial pattern. Thus, the Haversian structure is an adaptation only to high compressive stresses rendering its inferior tensile properties irrelevant as the regions with high tensile stresses have a non-Haversian, apparently primary microstructure (paper). |

|
|
Systems with purely hard core excluded volume interactions
are characterized by (i) no two particles may overlap and (ii) all
valid
configurations have equal energy. Thus, these systems are athermal and
any transitions, if present, are entropy driven. The simplest example is
a collection of hard spheres in three dimensions which freezes at
high density. When particles of different shapes are constrained to be
on lattices, then the models are called
hard core lattice gas models.
What are the possible phases when rods of length k are placed on square and triangular lattices? Each rod covers k consecutive sites along a lattice direction. For k larger than 6, the system undergoes two phase transitions when density is increased. Snapshots of the different phases are shown below. A paper describing a numerical study of the high-density transition and the high-density phase may be found here, a recent talk here, and a poster here. The phase transition from the low density disordered phase to the intermediate density nematic phase may be understood via a Bethe approximation (paper). Are the high density disordered and the low density disordered phases qualitatively the same? An exact calculation on a tree like lattice suggests that they are qualitatively similar. (paper) |

|
| Hard rectangles on lattices show a very rich phase diagram. For large enough aspect ratio, four different phases are seen at different densities. Snapshots of the different phases are shown below. |

|
| The phase diagram for rectangles of size 2x2k and 3x3k are shown below. The phase diagram is qualitatively similar for larger rectangles. A paper describing the hard rectangle system may be found here. |

|
|
Currently, we are studying systems of particles whose shapes are different from rods or rectangles. |
|
Sand, powder, and ball bearings are examples of granular systems.
Their dynamics is dominated by inelastic collisions. The large scale
effects of this feature can be obtained by studying
a gas of particles coming to rest through inelastic collisions. Such a
system is also known as the freely cooling granular gas.
How does the energy of a freely cooling granular gas decay with time?
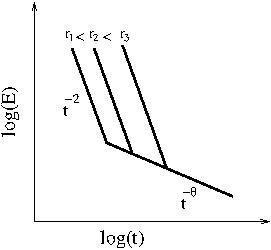
At initial times, the particles are homogeneously distributed and energy decreases as t-2. As time increases, the system coarsens into an inhomogeneous cooling regime wherein the energy dcreases as t-θ, where the exponent θ depends only on the dimension. A paper measuring θ in three dimensions may be found here. What is the nature of the coarsening process? We showed that the inhomogeneous cooling regime is further divided into two regimes. In the first, coarsening obeys Porod law and in the second it violates Porod law. See here and here for papers, and see here for a talk. The effective dynamics in the second regime is shown to be one of aggregation and fragmentation (paper).
A simpler problem is when all the particles are initially at rest, and
one particle is given an impulse, following which the system is
allowed to cool. When particles are inelastic, a moving shock front is
formed (see figure where the red denotes moving particles at a fixed
time)
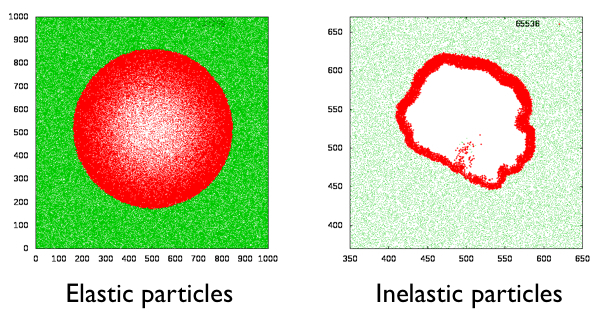
The exponent θ can be determined by a scaling argument and used to describe experiments on flowing granular systems (paper, paper, talk). |
| Under construction |
| Under construction |