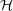 be a Hilbert space. Denote by U(
be a Hilbert space. Denote by U(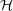 ) the
group of unitary automorphisms of
) the
group of unitary automorphisms of 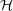 . Let U(1) denote the group
{z
. Let U(1) denote the group
{z  C : ∣z∣ = 1} under multiplication.
C : ∣z∣ = 1} under multiplication.
Let G be a finite group and let 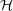 be a Hilbert space. Denote by U(
be a Hilbert space. Denote by U(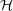 ) the
group of unitary automorphisms of
) the
group of unitary automorphisms of 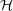 . Let U(1) denote the group
{z
. Let U(1) denote the group
{z  C : ∣z∣ = 1} under multiplication.
C : ∣z∣ = 1} under multiplication.
Definition 3.1 (Projective representation). A projective representation
of G on 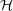 is a function η : G → U(
is a function η : G → U(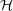 ) such that for every g,h
) such that for every g,h  G, there exists
a constant c(g,h)
G, there exists
a constant c(g,h)  U(1) such that
U(1) such that
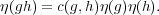 | (3.1) |
A projective representation where c(g,h) = 1 is a representation in the sense of Section 1.1 and, for emphasis, will be called an “ordinary representation”.
Exercise 3.2. Use the associative law on G to show that the function c : G × G → U(1) defined above satisfies the cocycle condition:
 | (3.2) |
It is natural to ask whether, given a projective representation η, is it
possible to find suitable scalars s(g)  U(1) for each g
U(1) for each g  G such that η(g)s(g) is
an ordinary representation. If such a set of scalars did exist, it would mean
that
G such that η(g)s(g) is
an ordinary representation. If such a set of scalars did exist, it would mean
that

 G. Applying (3.1) gives the coboundary condition:
G. Applying (3.1) gives the coboundary condition:
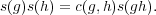
Observe that
Proposition 3.4. For any projective representation η of G, there exists a function s : G → U(1) such that η(g)s(g) is an ordinary representation if and only if the the cocycle defined by (3.1) is a coboundary.
Definition 3.5 (Central Extension). A central extension of G by U(1)
is a group  , together with a short exact sequence
, together with a short exact sequence
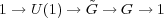
 .
.
Given a central extension  of G by U(1), pick any function s : G →
of G by U(1), pick any function s : G → (which may not be a homomorphism) such that the image of s(g) in G is
again g. Such a function is called a section. The failure of s to be a
homomorphism is measured by
(which may not be a homomorphism) such that the image of s(g) in G is
again g. Such a function is called a section. The failure of s to be a
homomorphism is measured by
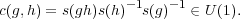 | (3.3) |
Exercise 3.6. Show that c(g,h) defined in (3.3) satisfies the cocycle condition (3.2). Moreover, if s is replaced by another section s′, and c′ is the resulting cocycle, then c′c-1 is a coboundary.
Thus a central extension of G by U(1) determines a well-defined element of H2(G,U(1)).
Exercise 3.7. Given a cocycle c : G × G → U(1) satisfying (3.2), show that G(c) = G × U(1) with multiplication defined by
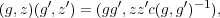
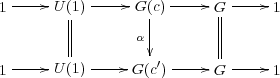
In this way, H2(G,U(1)) classifies the central extensions of G by U(1). Thus, H2(G,U(1)) arises in two different contexts:
The two are related in the following way:
Exercise 3.8. If η is a projective representation and c is the
cocycle associated to it by (3.1), then 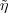 : G(c) → U(
: G(c) → U(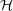 ) defined by
) defined by
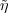 (g,z) = zη(g) defines an ordinary representation of G(c).
(g,z) = zη(g) defines an ordinary representation of G(c).
In other words, every projective representation can be resolved into an ordinary representation of the central extension corresponding to its cocycle.
Assume that the finite group G is abelian. Let L2(G) denote the Hilbert space obtained when the space of complex valued functions on G is endowed with the Hermitian inner product ∑ xf(x)g(x). On L2(G), there are two natural families of unitary operators:
| Translation operators: | (Txf)(y) = f(y - x), | x  G, G,
|
| Modulation operators: | (Mχf)(y) = χ(y)f(y), | χ  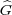 . . |
The translation operators give a unitary representation of G on the Hilbert
space L2(G). The modulation operators give a unitary representation of 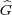 on the same space. However, these operators do not commute:
on the same space. However, these operators do not commute:
The commutator is a scalar. Thus the map η : G×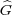 → U(L2(G)) defined
by
→ U(L2(G)) defined
by
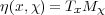
 on L2(G).
on L2(G).
Exercise 3.10. Show that the cocycle of G×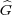 with coefficients in U(1)
associated to η in (3.1) is given by
with coefficients in U(1)
associated to η in (3.1) is given by
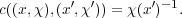 | (3.4) |
Definition 3.11 (Heisenberg group). The Heisenberg group H(G)
of G is the central extension of G ×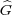 by U(1) corresponding to the
cocycle (3.4) (see Exercise 3.7).
by U(1) corresponding to the
cocycle (3.4) (see Exercise 3.7).
Explicitly, H(G) is the group whose underlying set of points is
G ×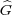 × U(1) with multiplication given by
× U(1) with multiplication given by
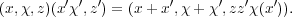 | (3.5) |
The projective representation η of G ×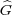 gives rise to an ordinary
representation
gives rise to an ordinary
representation 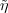 of H(G) on L2(G), known as the Heisenberg representation
(see Exercise 3.8). Explicitly, the Heisenberg representation is realized
as
of H(G) on L2(G), known as the Heisenberg representation
(see Exercise 3.8). Explicitly, the Heisenberg representation is realized
as
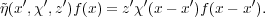 | (3.6) |
Remark 3.12. In the construction, and in all arguments relating to the Heisenberg group H(G), where G is a finite abelian group, U(1) can be replaced by an appropriate finite subgroup. Therefore, we may pretend that H(G) is a finite group.
Exercise 3.13. Verify that N := {0}×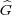 ×U(1) and
×U(1) and 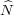 := G×{0}×U(1)
are normal subgroups of H(G). Z := {0}×{0}×U(1) is the centre of H(G).
Here 0 denotes the identity element of either G or
:= G×{0}×U(1)
are normal subgroups of H(G). Z := {0}×{0}×U(1) is the centre of H(G).
Here 0 denotes the identity element of either G or 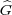 .
.
Let θ : N → C* be the character given by θ(0,χ,z) = z. Then the induced representation θH(G) is a representation of H(G) on the space
 | (3.7) |
The action of H(G) on I is given by g′f(g) = g(gg′). For each f  I,
define
I,
define 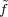 (x) = f(-x,0,1). Since the elements (-x,0,1), with x
(x) = f(-x,0,1). Since the elements (-x,0,1), with x  G form a
complete set of representatives of the cosets in N\H(G), f
G form a
complete set of representatives of the cosets in N\H(G), f
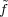 is an
isomorphism of I onto L2(G). Let g′ = (x′,χ′,z′) be an element of H(G)
is an
isomorphism of I onto L2(G). Let g′ = (x′,χ′,z′) be an element of H(G)
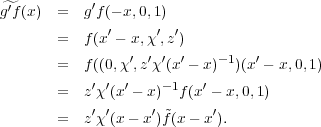
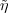 .
.
Let 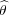 :
: 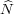 → C* be the character given by
→ C* be the character given by 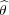 (x,0,z) = z. Then
(x,0,z) = z. Then 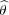 H(G) is a
representation of H(G) on the space
H(G) is a
representation of H(G) on the space
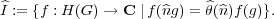

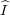 , define
, define 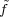 (χ) = f(0,-χ,1). Since the elements (0,-χ,1), with
χ
(χ) = f(0,-χ,1). Since the elements (0,-χ,1), with
χ 
 form a complete set of representatives of the cosets in
form a complete set of representatives of the cosets in 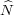 \H(G), f
\H(G), f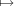
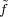 defines an isomorphism of
defines an isomorphism of 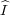 onto L2(
onto L2(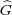 ).
).
Exercise 3.15. Show that the Fourier transform FT : L2(G) → L2(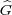 )
defined by
)
defined by
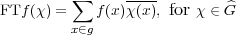
Theorem 3.16. The representation 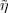 is irreducible. Every
irreducible representation of H(G) on which Z acts by the identity
character of U(1) is isomorphic to
is irreducible. Every
irreducible representation of H(G) on which Z acts by the identity
character of U(1) is isomorphic to 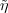 .
.
Proof. The irreducibility of 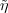 follows from the following exercise:
follows from the following exercise:
Exercise 3.17. Use Corollary 1.18 to show that θH(G) is irreducible.
Suppose that ρ is an irreducible representation of H(G) on which Z acts by the identity character of U(1). By Proposition 1.19,

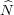 (ρ) consists of a single H(G)-orbit of characters of N. By hypothesis,
the restriction of all these characters to Z is the identity character of
U(1).
(ρ) consists of a single H(G)-orbit of characters of N. By hypothesis,
the restriction of all these characters to Z is the identity character of
U(1).
Exercise 3.18. Show that H(G) acts transitively on the set of characters of N1 whose restriction to Z is the identity character of U(1).
Therefore, θ 
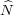 (ρ), and by Proposition 1.20, ρ
(ρ), and by Proposition 1.20, ρ θH(G). □
θH(G). □
Given an automorphism σ of H(G), let σ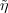 denote the representation of
H(G) on the representation space V η of η given by σ
denote the representation of
H(G) on the representation space V η of η given by σ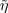 (g) =
(g) = 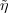 (σ-1
g). If σ fixes
every element of Z, then σ
(σ-1
g). If σ fixes
every element of Z, then σ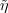 is also an irreducible representation of H(G) on
which Z acts by the identity character of U(1). By Theorem 3.16,
is also an irreducible representation of H(G) on
which Z acts by the identity character of U(1). By Theorem 3.16, 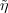 and σ
and σ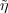 are equivalent. Therefore, there exists ν(σ) : V η → V η such
that
are equivalent. Therefore, there exists ν(σ) : V η → V η such
that
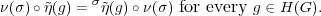 | (3.8) |
Moreover, by Schur’s lemma, ν(σ) is uniquely determined modulo a scalar. Let B0(G) denote the group of all automorphisms of H(G) which fix the elements of Z.
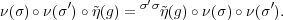
It follows that the map σ ρ(σ) = ν(σ-1) is a projective representation of
B0(G) on L2(G). Projective representations of subgroups of B0(G)
constructed in this way are known as Weil representations. In order to
construct ν(σ) it is helpful to think of the realization of
ρ(σ) = ν(σ-1) is a projective representation of
B0(G) on L2(G). Projective representations of subgroups of B0(G)
constructed in this way are known as Weil representations. In order to
construct ν(σ) it is helpful to think of the realization of 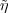 as θH(G). The
underlying vector space is the subspace I (see (3.7)) of C[H(G)]. Let
r denote the representation of H(G) on C[H(g)], where H(G) acts
by
as θH(G). The
underlying vector space is the subspace I (see (3.7)) of C[H(G)]. Let
r denote the representation of H(G) on C[H(g)], where H(G) acts
by
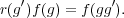
Exercise 3.21. If f  I, show that the function ν(σ)f defined
by
I, show that the function ν(σ)f defined
by
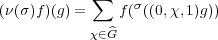 | (3.9) |
is also in I. The solution will use the fact that σ fixes every element of Z. Show that ν(σ) defined above satisfies (3.8).
Exercise 3.22. Let Q : G × → U(1) denote the map
→ U(1) denote the map
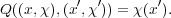
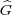 such that
such that
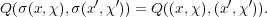
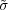 : H(G) → H(G) defined by
: H(G) → H(G) defined by
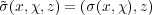
Exercise 3.23 (Symplectic form of the Heisenberg group).
Assume that x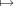 2x is an automorphism of G. Consider the bijection
φ : H(G) → G ×
2x is an automorphism of G. Consider the bijection
φ : H(G) → G ×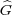 × U(1) given by
× U(1) given by
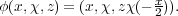
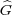 ×U(1))2 → G×
×U(1))2 → G× ×U(1) determined by the commutativity of
the diagram
×U(1) determined by the commutativity of
the diagram
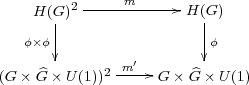
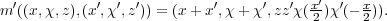 | (3.10) |
In this section SL2(Fq) will be realized as a subgroup of B0(G) for G = Fq2.
The resulting Weil representation will turn out to be an ordinary
representation (Proposition 3.26). All the cuspidal representations
of GL2(Fq) and SL2(Fq) will be found inside this representation in
Sections 3.5 and 3.6 respectively. Let G be the additive group of Fq2. The
map x (y
(y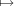 ψ(tr(xy))) defines an isomorphism of Fq2 onto
ψ(tr(xy))) defines an isomorphism of Fq2 onto  by
Proposition B.11. Using this identification, the Heisenberg group H(Fq2)
can be realized as Fq2 × Fq2 × U(1), with multiplication
by
Proposition B.11. Using this identification, the Heisenberg group H(Fq2)
can be realized as Fq2 × Fq2 × U(1), with multiplication

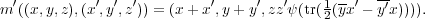
 yx))). Suppose σ =
yx))). Suppose σ = 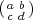
 SL2(Fq). Then if
Q((x,y),(x′,y′)) = tr(
SL2(Fq). Then if
Q((x,y),(x′,y′)) = tr( (yx′-y′x)),
(yx′-y′x)),
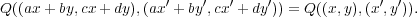

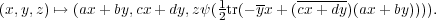 | (3.11) |
of the Heisenberg group H(G) in its usual coordinates.
Exercise 3.24. Show that in the action defined by (3.11), t(a) =  ,
when a
,
when a  Fq*, acts by
Fq*, acts by

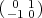 acts by
acts by
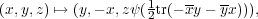
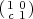 , when c
, when c  Fq, acts by
Fq, acts by
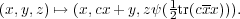
In the present context, (3.9) gives
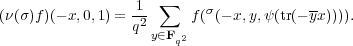
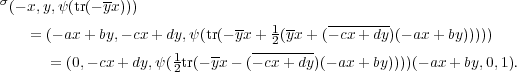 |

 |
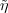 as L2(Fq2),
as L2(Fq2),
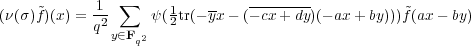
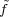
 L2(G), and therefore,
L2(G), and therefore,
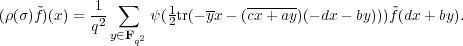 | (3.12) |
We have already seen that ρ : SL2(Fq) → GL(L2(Fq2)) is a projective
representation. Let 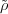 be the modification of ρ by scalars given by
be the modification of ρ by scalars given by
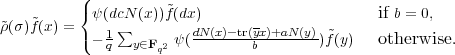 | (3.13) |
Proposition 3.26. The function 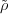 : SL2(Fq) → GL(L2(Fq)) defined
by (3.13) is an ordinary representation.
: SL2(Fq) → GL(L2(Fq)) defined
by (3.13) is an ordinary representation.
Proof. Suppose σ = 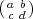 , σ′ =
, σ′ = 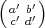 , and σ′′ =
, and σ′′ = 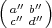 are elements
of SL2(Fq) such that σ′′ = σσ′. Let 10
are elements
of SL2(Fq) such that σ′′ = σσ′. Let 10  L2(Fq2) denote the indicator
function of {0}. In the case that b, b′ and b′′ are all non-zero, we
have
L2(Fq2) denote the indicator
function of {0}. In the case that b, b′ and b′′ are all non-zero, we
have
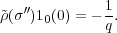
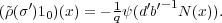
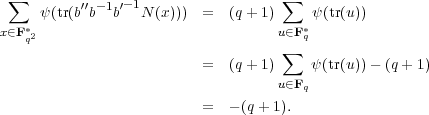
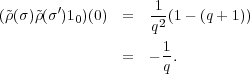
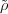 (σ′′) and
(σ′′) and 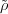 (σ)
(σ)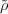 (σ′) differ by a scalar multiple.
It follows from the above calculations that this scalar multiple is
1.
(σ′) differ by a scalar multiple.
It follows from the above calculations that this scalar multiple is
1.
If b and b′ are non-zero, but b′′ = 0, then d′b′-1 + ab-1 = 0, and the
expression (3.14) equals 1, which is also the value of  (σ′′)10(0). Again, it
follows that
(σ′′)10(0). Again, it
follows that 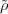 (σ′′) =
(σ′′) = 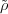 (σ)
(σ)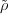 (σ′).
(σ′).
When exactly one of b and b′ is 0, then b′′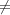 0. In these cases,
0. In these cases,
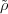 (σ)
(σ) (σ′) =
(σ′) = 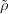 (σσ′) = -
(σσ′) = - . □
. □
Exercise 3.27. For a  Fq*, let t(a) =
Fq*, let t(a) =  , let w =
, let w = 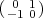 and for
c
and for
c  Fq, let u(c) =
Fq, let u(c) = 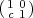 . Use (3.13) to show that for every
. Use (3.13) to show that for every 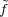
 L2(Fq2),
L2(Fq2),
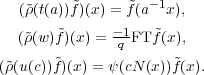 | (3.15) (3.16) (3.17) |
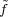
 L2(Fq2) is once again
thought of as a function of Fq2, since Fq2 is identified with its Pontryagin
dual. Explicitly,
L2(Fq2) is once again
thought of as a function of Fq2, since Fq2 is identified with its Pontryagin
dual. Explicitly,
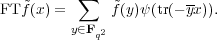
Exercise 3.28. Any element of SL2(Fq) can be written as a
product of elements of the above types. Consider the matrix 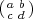
 SL2(Fq). If b = 0, then d = a-1 and
SL2(Fq). If b = 0, then d = a-1 and 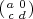 = t(a)u(ac). On the other hand,
if b
= t(a)u(ac). On the other hand,
if b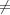 0, then
0, then 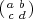 = u(d∕b)wu(ab)t(b-1).
= u(d∕b)wu(ab)t(b-1).
In Chapter 2 we constructed all the representations (π,V ) of GL2(Fq) for which
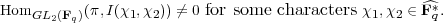
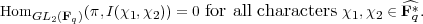 | (3.18) |
Representations (π,V ) satisfying (3.18) are known as the cuspidal representations of GL2(Fq). By Frobenius reciprocity (Section 1.3), we have
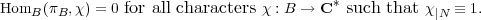
Given a representation (π,V ) of any group G, let V * be the dual space HomC(V,C) of V . Let π* be the representation of G on V * given by

Proposition 3.29. A representation (π,V ) of GL2(Fq) is cuspidal if
and only if there exists no non-zero vector ξ  V * such that
V * such that
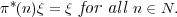 | (3.19) |
Proof. Suppose (π,V ) is not cuspidal. Then there exists a non-zero
element ξ  HomB(V,χ) for some χ : B → C* such that χ∣N ≡ 1. Such a ξ can
be regarded as an element of V *. We have, for any n
HomB(V,χ) for some χ : B → C* such that χ∣N ≡ 1. Such a ξ can
be regarded as an element of V *. We have, for any n  N and v
N and v  V ,
V ,
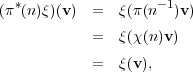
Conversely, look at the space V *N of all vectors in V * satisfying (3.19).
This space is preserved under the action of T (since tNt-1 = N for all t  T).
Therefore, one can write
T).
Therefore, one can write
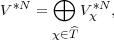
 V *N which transform under T by χ. If
V *N
V *N which transform under T by χ. If
V *N 0, then there exists χ such that V χ*N
0, then there exists χ such that V χ*N 0. Therefore, HomB(V,χ)
0. Therefore, HomB(V,χ)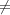 0,
from which it follows that (π,V ) is not cuspidal. □
0,
from which it follows that (π,V ) is not cuspidal. □
Corollary 3.31. The degree of every cuspidal representation of GL2(Fq) is always a multiple of (q - 1).
Proof. Suppose that (π,V ) is a cuspidal representation. For each
a  Fq, let V a* be the space of all ξ
Fq, let V a* be the space of all ξ  V * such that
V * such that
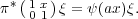
 Fq*. Hence for a
Fq*. Hence for a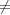 0, the
q - 1 spaces V *(ta), with t
0, the
q - 1 spaces V *(ta), with t  Fq* have the same dimension. The space V *(0) is
just V *(N), hence is trivial. Therefore the dimension of V *, hence the degree
of V must be a multiple of q - 1. □
Fq* have the same dimension. The space V *(0) is
just V *(N), hence is trivial. Therefore the dimension of V *, hence the degree
of V must be a multiple of q - 1. □
From Corollary 3.31 and the discussion at the end of Section 2.3 it
follows that besides the representations constructed in that section, there
are exactly  (q2 - q) irreducible cuspidal representations, each of degree
q - 1. These representations are constructed in Section 3.5.
(q2 - q) irreducible cuspidal representations, each of degree
q - 1. These representations are constructed in Section 3.5.
A cuspidal representation of SL2(Fq) can be defined in a similar manner. A representation (π,V ) of SL2(Fq) is said to be cuspidal if
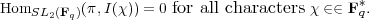
Exercise 3.32. Verify that Proposition 3.29 continues to hold when GL2(Fq) is replaced by SL2(Fq).
However, Corollary 3.31 does not hold as stated
Exercise 3.33. Show that the degree of a cuspidal representation
of SL2(Fq) is always a multiple of 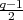 .
.
Let ω be a character of Fq2* such that ω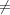 χ ∘ N for any character χ of Fq*
(here N denotes the norm map Fq2 → Fq). Such a character is called
primitive.
χ ∘ N for any character χ of Fq*
(here N denotes the norm map Fq2 → Fq). Such a character is called
primitive.
Let
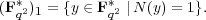
Exercise 3.35. Show that a character ω : Fq2* → C* is primitive if and only if its restriction to (Fq2*)1 is non-trivial.
Define
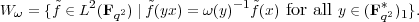
Exercise 3.36. Show that Wω is preserved by the action of 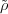 (σ)
for every σ
(σ)
for every σ  SL2(Fq). [Hint: note that if N(x) = 1, then x = x-1.]
SL2(Fq). [Hint: note that if N(x) = 1, then x = x-1.]
Therefore, 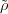 gives a representation (πω,Wω) for each such ω. For any
x
gives a representation (πω,Wω) for each such ω. For any
x  Fq2, the set of elements x′ such that N(x′) = N(x) coincides with the set
of elements of the form x′′x, where x′′
Fq2, the set of elements x′ such that N(x′) = N(x) coincides with the set
of elements of the form x′′x, where x′′ (Fq2*)1. Hence, if f
(Fq2*)1. Hence, if f  Wω, then the
value of
Wω, then the
value of 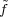 at x determines the value of
at x determines the value of 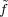 at any element x′ with
N(x′) = N(x). However, if x = 0, there is an additional constraint, namely
that
at any element x′ with
N(x′) = N(x). However, if x = 0, there is an additional constraint, namely
that 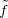 (0) = ω(y)-1
(0) = ω(y)-1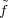 (0) for every y
(0) for every y  (Fq2*)1. By Exercise 3.35, if ω is
primitive, then it is forced that
(Fq2*)1. By Exercise 3.35, if ω is
primitive, then it is forced that 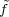 (0) = 0. Since there are q - 1 non-zero values
for the norm, we have
(0) = 0. Since there are q - 1 non-zero values
for the norm, we have
Each matrix σ in GL2(Fq) can be written in a unique way as a product of
 and a matrix in SL2(Fq). Define
and a matrix in SL2(Fq). Define
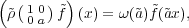 | (3.20) |
where ã  Fq2* is chosen so that N(ã) = a.
Fq2* is chosen so that N(ã) = a.
Exercise 3.38. Check that the right hand side of (3.20) does not depend on the choice of ã such that N(ã) = a, and that it preserves Wω for each primitive ω.
Extend πω to GL2(Fq) by 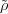
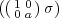 =
= 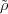

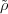 (σ). For this extended
function to be a homomorphism of groups, it is necessary that, for all
a,a′
(σ). For this extended
function to be a homomorphism of groups, it is necessary that, for all
a,a′ Fq* and all σ,σ′
Fq* and all σ,σ′ SL2(Fq),
SL2(Fq),
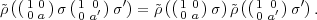 | (3.21) |
But
![[( ) ]
(1 0)σ (1 0′)σ′ = (1 0′) 1 ′0-1 σ(1 0′) σ′ ,
0 a 0 a 0 aa 0 a 0 a](notes356x.png)
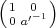 σ
σ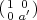 σ′
σ′ SL2(Fq).
SL2(Fq).
Exercise 3.39. Using this to expand both sides of (3.21) in terms of
(3.20), show that it is sufficient to check that for each a  Fq*, f
Fq*, f  L2(Fq2)
and each element σ of SL2(Fq),
L2(Fq2)
and each element σ of SL2(Fq),
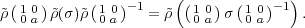 | (3.22) |
Exercise 3.40. Verify (3.22) for σ of the form t(a), w and u(c) (see
Exercise 3.28). Conclude that it holds for all σ  SL2(Fq).
SL2(Fq).
We will denote again by (πω,Wω) the restriction of 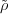 to the subspace
Wω.
to the subspace
Wω.
Proof. We will show that Wω contains no non-zero vectors fixed by N,
the subgroup consisting of matrices of the form 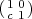 , c
, c  Fq. This suffices,
for
Fq. This suffices,
for 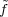 is fixed by N if and only if πω(w)
is fixed by N if and only if πω(w)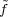 is fixed by N. Suppose that
is fixed by N. Suppose that
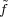 0 is a vector fixed by N. By Lemma 3.37,
0 is a vector fixed by N. By Lemma 3.37, 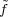 0(0) = 0. On the other
hand, if x
0(0) = 0. On the other
hand, if x  Fq2*, then choose c
Fq2*, then choose c  Fq so that ψ(cN(x))
Fq so that ψ(cN(x))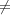 1. Then, by
(3.17)
1. Then, by
(3.17)
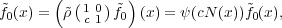
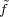 0(x) = 0. □
0(x) = 0. □
Clearly, any sub-representation of a cuspidal representation is also cuspidal. Therefore, by Corollary 3.31 (πω,Wω) is simple for each ω of the type considered above.
Lemma 3.42. Let ω and η be two characters of Fq2* as above. If the representations (πω,Wω) and (πη,Wη) are isomorphic, then either ω = η or ω = η ∘ F, where F is the Frobenius automorphism Fq2* → Fq2* (see Section B.3).
Proof. For each u  Fq*, fix an element ũ
Fq*, fix an element ũ  Fq2 such that N(ũ) = u.
Let 1u
Fq2 such that N(ũ) = u.
Let 1u  Wω be the unique function such that 1u(ũ) = 2 and 1u(x) = 0
if N(x)
Wω be the unique function such that 1u(ũ) = 2 and 1u(x) = 0
if N(x)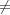 u. The set {1u ∣ u
u. The set {1u ∣ u  Fq*} is a basis of Wω. Therefore, for any
σ
Fq*} is a basis of Wω. Therefore, for any
σ  GL2(Fq), tr(πω(σ)) = ∑
u
GL2(Fq), tr(πω(σ)) = ∑
u Fq*(πω(σ)1u)(ũ).
Fq*(πω(σ)1u)(ũ).
For any a  Fq2*,
Fq2*, 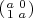 =
= 
 . From (3.13) and (3.20), we
have that
. From (3.13) and (3.20), we
have that

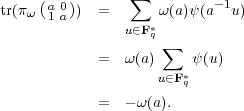
Exercise 3.43. Show that if ω and η are two characters of Fq2*, then their restrictions to Fq* are equal if and only if either ω = η or ω = η ∘ F.
If (πω,Wω) and (πη,Wη) were isomorphic, then we would have

Let ω be a non-trivial character if (Fq*)1, the subgroup of Fq* consisting of elements of norm one (there are exactly q such characters). As in section 3.5 define
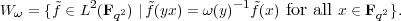
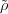 of SL2(Fq) on L2(Fq2).
Each such representation is of dimension q - 1. Let πω denote the
representation of SL2(Fq) on Wω. These are just the restrictions of the
representations of GL2(Fq) constructed in Section 3.5 to SL2(Fq). It
follows that they are cuspidal. However, it no longer follows that
these representations are irreducible, as the degree of a cuspidal
representation of SL2(Fq) is only known to be a multiple of
of SL2(Fq) on L2(Fq2).
Each such representation is of dimension q - 1. Let πω denote the
representation of SL2(Fq) on Wω. These are just the restrictions of the
representations of GL2(Fq) constructed in Section 3.5 to SL2(Fq). It
follows that they are cuspidal. However, it no longer follows that
these representations are irreducible, as the degree of a cuspidal
representation of SL2(Fq) is only known to be a multiple of 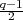 by
Exercise 3.33.
by
Exercise 3.33.
We shall analyze the representations πω through their characters. We
already know that tr(πω(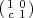 )) = -1 from the proof of Lemma 3.43.
)) = -1 from the proof of Lemma 3.43.
Lemma 3.45. For every character ω of (Fq2*)1 and d  Fq such that
λ2 - dλ + 1 is irreducible with roots z and z-1 in Fq2,
Fq such that
λ2 - dλ + 1 is irreducible with roots z and z-1 in Fq2,

Proof. By (3.13), we have
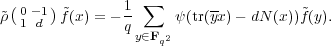
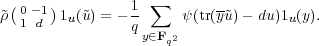
 (Fq2*)1. We have
(Fq2*)1. We have 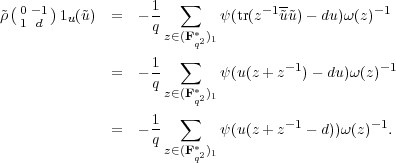
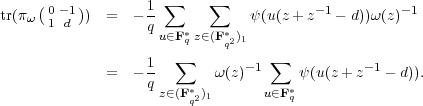
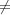 z + z-1, then
z + z-1, then
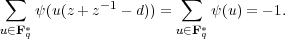

![(0 -1) 1 ∑ -1 1 ∑ -1
tr(π ω 1 d ) = - q ω(z) (q+ 1)- q ω(z)
z[+z-1=d z+z-1⁄=]d
1 ∑ -1 ∑ -1
= - q * ω(z) + qω(z)
z∈Fq2 z+z-1=d
= - ω(z) - ω(z)-1.](notes390x.png)
Exercise 3.46. Suppose that ω is the unique non-trivial character
of (Fq2*)1 taking only the values ±1. Show that ∑
σ SL2(Fq)tr(πω(σ)) =
2(q3-q). Conclude that πω(σ) is a sum of two non-isomorphic irreducible
representations of SL2(Fq).
SL2(Fq)tr(πω(σ)) =
2(q3-q). Conclude that πω(σ) is a sum of two non-isomorphic irreducible
representations of SL2(Fq).
These representations must be irreducible of degree 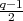 by Exercise 3.33.
Using the book-keeping at the end of Section 2.5, we see that there remain
by Exercise 3.33.
Using the book-keeping at the end of Section 2.5, we see that there remain
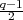 irreducible representations of SL2(Fq).
irreducible representations of SL2(Fq).
Exercise 3.47. Define an equivalence relation on the set of non-trivial characters of (Fq2*)2 by ω ~ ω′, where ω′ = ω∘F. Here F is the Frobenius automorphism (Section B.3). Observe that tr(πω) = tr(πω′). Show that the characters of the representations πω, where ω runs over the equivalence classes of non-trivial characters of (Fq2*)1 are pairwise orthogonal.
It follows that πω, ω non-trivial and different from the character considered
in Exercise 3.46 give the remaining 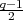 irreducible representations of
SL2(Fq).
irreducible representations of
SL2(Fq).