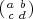 in GL2(Fq) consider its characteristic polynomial
in GL2(Fq) consider its characteristic polynomial
Given a matrix 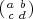 in GL2(Fq) consider its characteristic polynomial
in GL2(Fq) consider its characteristic polynomial
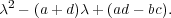
To summarise, the conjugacy classes in GL2(Fq) are as follows:
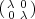 , with λ
, with λ  Fq*.
Fq*.
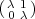 , with λ
, with λ  Fq*.
Fq*.
 (q - 1)(q - 2) classes represented by
(q - 1)(q - 2) classes represented by 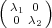 with λ1
with λ1 λ2.
λ2.
 (q2 - q) classes represented by
(q2 - q) classes represented by 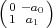 , with λ2 - a1λ + a0 an
irreducible polynomial in Fq[t].
, with λ2 - a1λ + a0 an
irreducible polynomial in Fq[t].In all, there are
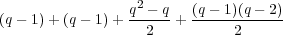 | (2.1) |
conjugacy classes. Detailed information about the conjugacy classes is collected in Table 1.
|
Let B be the subgroup of GL2(Fq) consisting of invertible upper triangular matrices. Let N be the subgroup of upper triangular matrices with 1’s along the diagonal. Let T be the subgroup of invertible diagonal matrices.
Let w =  .
.
Note that B is really a double coset B1B. So Proposition 2.5 really tells us that the double coset space B\GL2(Fq)∕B has two elements and that {1,w} is a complete set of representatives for these double cosets.
Proof. A matrix 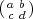 lies in B if and only if c = 0. If c
lies in B if and only if c = 0. If c 0,
then
0,
then
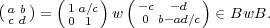
Given characters χ1 and χ2 of Fq*, we get a character χ of T by
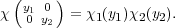
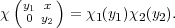 | (2.2) |
Let I(χ1,χ2) be the representation of GL2(Fq) induced from this character of B.
Proof. Let χ and μ be the characters of B obtained from the pairs χ1, χ2 and μ1, μ2 respectively as in (2.2). We regard χ and μ as one-dimensional representations of B acting on the space C. We may identify HomC(C,C) with C as well. Then, using Mackey’s description of intertwiners (Theorem 1.12), we see that we must compute the dimension of the space of functions Δ : GL2(Fq) → C such that
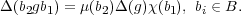 | (2.3) |
It follows from the Bruhat decomposition that Δ is completely determined by its values at 1 and w.
Taking g = 1 in (2.3), we see that for any t  T,
T,
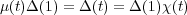
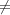 χ then Δ(1) = 0. On the other hand, if μ = χ, let Δ1 be the
function such that
χ then Δ(1) = 0. On the other hand, if μ = χ, let Δ1 be the
function such that
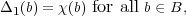
Taking g = w in (2.3), we see that for any t  T,
T,
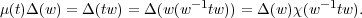
Therefore, if μ1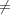 χ2 or μ2
χ2 or μ2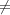 χ1 then Δ(w) = 0. On the other hand, if
μ1 = χ2 and μ2 = χ1, let Δw be the function such that
χ1 then Δ(w) = 0. On the other hand, if
μ1 = χ2 and μ2 = χ1, let Δw be the function such that
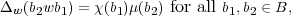
An arbitrary functions satisfying (2.3) can be expressed as a linear combination of Δ1 and Δw, so we see that the dimension of the space of such functions must be e1 + ew. □
Theorem 2.8. Let χ1, χ2, μ1 and μ2 be characters of Fq*. Then I(χ1,χ2) is an irreducible representation of degree q + 1 of GL2(Fq) unless χ1 = χ2, in which case it is a direct sum of two irreducible representations having degrees 1 and q. We have
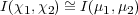
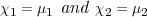 | (2.4) |
or else
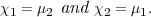 | (2.5) |
Proof. Apply Proposition 2.6 with χ1 = μ1 and χ2 = μ2. We see that
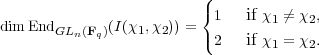
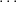 ,πh with multiplicities
m1,
,πh with multiplicities
m1,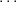 ,mh and with degrees d1,
,mh and with degrees d1,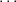 ,dh respectively, then the dimension of
EndG(V ) is ∑
midi2. Hence I(χ1,χ2) is irreducible if χ1
,dh respectively, then the dimension of
EndG(V ) is ∑
midi2. Hence I(χ1,χ2) is irreducible if χ1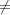 χ2, otherwise it is a
direct sum of two irreducible representations because 2 = 12 + 12 is the only
way of writing 2 as a sum of non-zero multiples of more than one non-zero
squares.
χ2, otherwise it is a
direct sum of two irreducible representations because 2 = 12 + 12 is the only
way of writing 2 as a sum of non-zero multiples of more than one non-zero
squares.
Because the index of B in GL2(Fq) is q + 1, the dimension of I(χ1,χ2) is
always q + 1. If χ1 = χ2, the representation of GL2(Fq) generated by the
function f(g) = χ1(det(g)) clearly satisfies f(bg) = χ(b)f(g) for all b  B and
g
B and
g  G. Therefore f
G. Therefore f  I(χ1,χ2). Moreover, (g ⋅f)(x) = χ1(det(g))f. Therefore the
one-dimensional subspace spanned by f is invariant under the action of G,
hence forms a one-dimensional representation of G. The other component is
therefore q-dimensional.
I(χ1,χ2). Moreover, (g ⋅f)(x) = χ1(det(g))f. Therefore the
one-dimensional subspace spanned by f is invariant under the action of G,
hence forms a one-dimensional representation of G. The other component is
therefore q-dimensional.
If χ1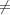 χ2 then, I(χ1,χ2) is irreducible. By Proposition 2.6 there exists a
non-zero element in Hom(I(χ1,χ2),I(μ1,μ2)) if and only if χ1 = μ1 and
χ2 = μ2 or χ1 = μ2 and χ2 = μ1. By irreducibility, these homomorphisms
must be isomorphisms. This proves the second part of the theorem.
□
χ2 then, I(χ1,χ2) is irreducible. By Proposition 2.6 there exists a
non-zero element in Hom(I(χ1,χ2),I(μ1,μ2)) if and only if χ1 = μ1 and
χ2 = μ2 or χ1 = μ2 and χ2 = μ1. By irreducibility, these homomorphisms
must be isomorphisms. This proves the second part of the theorem.
□
To summarise, in this section, we have constructed irreducible representations of GL2(Fq) corresponding to characters χ = (χ1,χ2) of T:
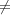 χ2, there is a unique irreducible representation of
GL2(Fq) of degree q + 1 corresponding to χ; the irreducible
representation corresponding to (χ1,χ2) is isomorphic to the
one corresponding to (χ2,χ1). We have
χ2, there is a unique irreducible representation of
GL2(Fq) of degree q + 1 corresponding to χ; the irreducible
representation corresponding to (χ1,χ2) is isomorphic to the
one corresponding to (χ2,χ1). We have  (q-1)(q-2) irreducible
representations of degree q + 1.
(q-1)(q-2) irreducible
representations of degree q + 1.
Recall from Schur theory, that the number of irreducible representations is the same as the number of conjugacy classes in a group. We have constructed
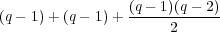
 (q2 - q) representations left to construct.
(q2 - q) representations left to construct.
Recall that for a group of order n whose irreducible representations are π1,…,πr of degrees d1,…,dr respectively,
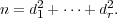
The sum of squares of degrees of the representations that we have constructed so far is
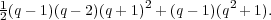
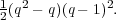
We will see in Section 3.4 that there are  (q2 - q) irreducible
representations of degree q - 1 remaining. These will be constructed in
Section 3.5.
(q2 - q) irreducible
representations of degree q - 1 remaining. These will be constructed in
Section 3.5.
Let Aut(SL2(Fq)) denote the group of all automorphisms of SL2(Fq). GL2(Fq) acts on SL2(Fq) by conjugation. This gives rise to a homomorphism GL2(Fq) → Aut(SL2(Fq)). The kernel of this automorphism consists of scalar matrices in GL2(Fq), and is therefore isomorphic to Fq*. The image is therefore isomorphic to the group PGL2(Fq), which is the quotient of GL2(Fq) by the subgroup of invertible scalar matrices. The orbits of PGL2(Fq) on SL2(Fq) are precisely the conjugacy classes of GL2(Fq) which are contained in SL2(Fq) (note that SL2(Fq) is a union of conjugacy classes of GL2(Fq)).
On the other hand, the image of SL2(Fq) in Aut(SL2(Fq)) is PSL2(Fq), the quotient of SL2(Fq) by the subgroup {±1}. The conjugacy classes of SL2(Fq) are precisely the PSL2(Fq) orbits.
Now, PSL2(Fq) is a subgroup of PGL2(Fq) (when both groups are viewed
as subgroups of Aut(SL2(Fq))) of index two. Therefore, each conjugacy class
of GL2(Fq) whose elements lie in SL2(Fq) is either a single conjugacy class in
SL2(Fq) or a union of two conjugacy classes in SL2(Fq). If ε is an element of
Fq* which is not a square (since q is assumed to be odd, there are 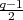 such
elements), then the image of
such
elements), then the image of  in Aut(SL2(Fq)) does not lie in the image
of SL2(Fq).
in Aut(SL2(Fq)) does not lie in the image
of SL2(Fq).
Let σ  SL2(Fq). Whether or not the conjugacy class of σ in GL2(Fq)
splits or not can be determined by counting. The basic principle here is that
the number of elements in an orbit for a group action is the index of the
stabiliser of a point in the orbit.
SL2(Fq). Whether or not the conjugacy class of σ in GL2(Fq)
splits or not can be determined by counting. The basic principle here is that
the number of elements in an orbit for a group action is the index of the
stabiliser of a point in the orbit.
With the above observations in mind, it is not difficult to prove that
Theorem 2.11. Let σ  SL2(Fq). Let Z denote the centraliser of σ
in GL2(Fq). Then [Z : Z ∩ SL2(Fq)] is either q - 1 or
SL2(Fq). Let Z denote the centraliser of σ
in GL2(Fq). Then [Z : Z ∩ SL2(Fq)] is either q - 1 or 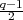 . In the former
case, the conjugacy class of σ in GL2(Fq) is a single conjugacy class in
SL2(Fq). In the latter case, the conjugacy class of σ in GL2(Fq) is a union
of two conjugacy classes in SL2(Fq), represented by σ and
. In the former
case, the conjugacy class of σ in GL2(Fq) is a single conjugacy class in
SL2(Fq). In the latter case, the conjugacy class of σ in GL2(Fq) is a union
of two conjugacy classes in SL2(Fq), represented by σ and  σ
σ -1
respectively.
-1
respectively.
Exercise 2.12. Prove Theorem 2.11.
In all, there are
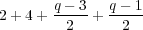 | (2.6) |
conjugacy classes.
|
Let B now consist of the upper triangular matrices in SL2(Fq), N the upper triangular matrices with 1’s along the diagonal, and T the matrices in SL2(Fq) which are diagonal. Note that the results of Exercise 2.4 are still valid, as is the Bruhat decomposition:
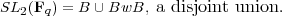
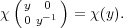
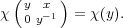
Taking μ = χ in Proposition 2.14 gives that
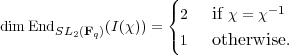
 Fq* to be a generator (this is cyclic of even order q - 1 by
Theorem B.5). Note that χ is completely determined by χ(ε), which can be
any (q - 1)st root of unity in C*. Furthermore, χ = χ-1 if and only
if χ(ε) = χ(ε)-1, i.e., if and only if χ(ε) = ±1. Therefore, there are
q - 3 characters χ for which I(χ) is irreducible. For each of these,
I(χ)
Fq* to be a generator (this is cyclic of even order q - 1 by
Theorem B.5). Note that χ is completely determined by χ(ε), which can be
any (q - 1)st root of unity in C*. Furthermore, χ = χ-1 if and only
if χ(ε) = χ(ε)-1, i.e., if and only if χ(ε) = ±1. Therefore, there are
q - 3 characters χ for which I(χ) is irreducible. For each of these,
I(χ) I(χ-1), and there are no other isomorphic pairs. We get
I(χ-1), and there are no other isomorphic pairs. We get 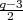 such irreducible representations, each of degree q + 1. There remain
the characters χ for which χ(ε) = ±1. Each of these give rise to two
irreducible non-isomorphic representations. We consider the two cases
separately:
such irreducible representations, each of degree q + 1. There remain
the characters χ for which χ(ε) = ±1. Each of these give rise to two
irreducible non-isomorphic representations. We consider the two cases
separately:
In this case, I(χ) contains the invariant one dimensional subspace of constant functions on G. Therefore I(χ) splits into a direct sum of two irreducible representations, the trivial representation and a representation of dimension q, which is called the Steinberg representation.
In this case it is necessary to make a closer analysis of EndSL2(Fq)(I(χ)). Let Δ1 denote the unique function SL2(Fq) → C for which Δ1(1) = 1, Δ1(w) = 0, and Δ(b1gb2) = χ(b1)Δ(g)χ(b2). Also let Δw denote the unique function SL2(Fq) → C for which Δw(1) = 0, Δw(w) = 1, and Δ(b1gb2) = χ(b1)Δ(g)χ(b2). These two functions form a basis of EndSL2(Fq)(I(χ)). Write I(χ) = ρ+ ⊕ ρ-, where ρ+ and ρ- are the two irreducible summands of of I(χ). The identity endomorphism in I(χ) can be written as a sum of two idempotents, coming from the identity endomorphisms of ρ+ and ρ-.
| Δ1 * Δ1 = q(q - 1)Δ1, | Δ1 * Δw = q(q - 1)Δw, | ||
| Δw * Δ1 = q(q - 1)Δw, | Δw * Δw = q2(q - 1)χ(-1)Δ1. |
Exercise 2.17. Besides q-1(q - 1)-1Δ1 and 0, show that the only idempotents in EndSL2(Fq)(I(χ)) are
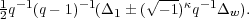
Let εI(χ) be the representation of SL2(Fq) on the representation space of I(χ), but where the action of SL2(Fq) is given by
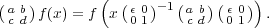
Therefore, the two representations ρ+ and ρ- must have equal degrees.
It follows that I(χ) is a sum of two irreducible representations, each of
degree 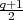 .
.
In this section, we have constructed
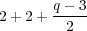
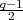 irreducible representations to construct. The sums of
squares of the degrees of the representations that we have constructed so far
is:
irreducible representations to construct. The sums of
squares of the degrees of the representations that we have constructed so far
is:
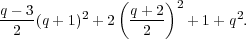
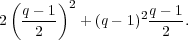
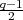 , and
, and 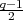 of degree
q - 1.
of degree
q - 1.