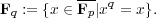
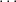 1 (n times) is 0). Therefore, it contains
one of the finite fields Fp. This makes it a finite dimensional vector space
over Fp, so that its order must be some power of p. We will see that, up to
isomorphism, there is exactly one field of a given prime power order. We
will also show that choosing a non-trivial character of the additive
group of a finite field gives an identification of this group with its
Pontryagin dual, and we will study the Fourier transform in this
context.
1 (n times) is 0). Therefore, it contains
one of the finite fields Fp. This makes it a finite dimensional vector space
over Fp, so that its order must be some power of p. We will see that, up to
isomorphism, there is exactly one field of a given prime power order. We
will also show that choosing a non-trivial character of the additive
group of a finite field gives an identification of this group with its
Pontryagin dual, and we will study the Fourier transform in this
context.
We will show that for any power pk of p, there is a unique finite field of order pk, which is unique up to isomorphism1 . For convenience, write q = pk. Fix an algebraic closure Fp of Fp. Look at the set
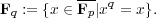
It follows from the above exercise that Fq is a field (why?).
Exercise B.2. Let K be any field, and f(X)  K[X] be of degree
d. Show that f(X) can not have more than d roots in K.
K[X] be of degree
d. Show that f(X) can not have more than d roots in K.
Since the elements of S are roots of the polynomial Xq - X which has degree q, there can be no more than q of them.
Exercise B.3. Let K be any field. For a polynomial f(X)  K[X]
K[X]
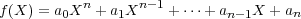
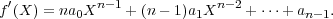
The derivative of the polynomial Xq -X is the constant polynomial -1. Therefore, all its roots in Fp are distinct. This means that S has exactly q elements. Therefore there exists a subfield of order q in Fp. In particular there exists a finite field of order q.
On the other hand, in any field of order q, the multiplicative group of non-zero elements in the field has order q - 1. Therefore, each element of the field satisfies xq-1 = 1, or xq = x. Thus any subfield of Fq of order q must be equal to S.
Now any field of order q must have characteristic p, hence is an algebraic extension of Fp. Therefore, it is isomorphic to some subfield of Fp. We have seen that only such field is Fq. It follows that every field of order q is isomorphic to Fq. We have proved the following theorem:
Theorem B.4. For every power q of a prime number, there exists a finite field of order q, which is unique up to isomorphism.
We present the proof of the following theorem straight out of Serre’s book [Ser73].
Proof. If d is an integer ≥ 1, then let φ(d) denote the number of integers x with 1 ≤ x ≤ d such that (x,d) = 1. In other words, the image of x in Z∕dZ is a generator of Z∕dZ. The function φ(d) is called the Euler totient function.
Proof. If d∣n, let Cd denote the unique subgroup of order d in Z∕nZ, and Φd denote the generators of Cd. Then Z∕nZ is the disjoint union of the Φd. Φd had φ(d) elements. Adding up cardinalities, n = ∑ d∣nφ(d). □
Lemma B.7. Let H be a finite group of order n. Suppose that, for all divisors d of n the set
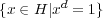
Proof. Let d∣n. If there exists x  H of order d, the subgroup
H of order d, the subgroup
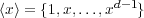
To complete the proof of Theorem B.5, note that the equation xd = 1 is a polynomial equation, and hence, by Exercise B.2 has at most d solutions in Fq. □
In general, if E is an extension of a field F, then every element x  E can be
thought of as an F-linear endomorphism of the F-vector space E, when
it acts on E by multiplication. The trace of this map is denoted
tr
E∕F(x). The function trE∕F : E → F is called the trace function of E
over F. Likewise, the determinant of multiplication by x is denoted
NE∕F (x). The function NE∕F : E → F is called the norm map of E over
F.
E can be
thought of as an F-linear endomorphism of the F-vector space E, when
it acts on E by multiplication. The trace of this map is denoted
tr
E∕F(x). The function trE∕F : E → F is called the trace function of E
over F. Likewise, the determinant of multiplication by x is denoted
NE∕F (x). The function NE∕F : E → F is called the norm map of E over
F.
Since Fq2 is a quadratic extension of Fq, its Galois group is cyclic
of order 2. Clearly, the map F : x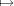 xp is an automorphism of Fq2
that fixes Fq. Therefore, it must be the non-trivial element in the
Galois group of Fq2 over Fq. F is called the Frobenius automorphism.
In analogy with complex conjugation, we write F(x) = x for each
x
xp is an automorphism of Fq2
that fixes Fq. Therefore, it must be the non-trivial element in the
Galois group of Fq2 over Fq. F is called the Frobenius automorphism.
In analogy with complex conjugation, we write F(x) = x for each
x  Fq2.
Fq2.
Let N and tr denote the norm and trace maps of Fq2 over Fq respectively. Then

 Fq2, N(x) = 0 if and only if x = 0.
Fq2, N(x) = 0 if and only if x = 0.
Exercise B.10. Show that the norm map N : Fq2*→ Fq* is surjective.
Conclude that for any x  Fq, the number of elements y
Fq, the number of elements y  Fq2 such that
N(y) = x is
Fq2 such that
N(y) = x is
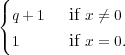
Let ψ0 : Fq → C* be a non-trivial additive character. Such a character is completely determined by its value at 1, which can be any pth root of unity different from 1. Then ψ : Fq → C* defined by ψ(x) = ψ(trFq∕Fp(x)) is a non-trivial additive character of Fq.
Proposition B.11. For each x′  Fq, set ψx′(x) = ψ(x′x). Then
x′
Fq, set ψx′(x) = ψ(x′x). Then
x′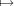 ψx′ is an isomorphism from the additive group of Fq onto its
Pontryagin dual.
ψx′ is an isomorphism from the additive group of Fq onto its
Pontryagin dual.
Proof. The map x′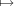 ψx′ is clearly an injective homomorphism. By
Proposition 1.2, it must also be onto. □
ψx′ is clearly an injective homomorphism. By
Proposition 1.2, it must also be onto. □