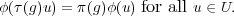
Let G be a finite group. A representation of G on a vector space V is a pair (π,V ) where V is a complex vector space and π is a homomorphism G → GL(V ). Often, we will denote (π,V ) simply by π, specially when the vector space V is specified implicitly. The dimension of V is called the degree of the representation (π,V ). In these notes all representations will be assumed to be of finite degree. If (π,V ) and (τ,U) are two representations of G, then a linear map φ : U → V is called a homomorphism of G-modules, or an intertwiner if
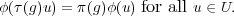
Let G be an abelian group. The binary operation on the group will be
written additively. A character of G is a homomorphism χ : G → C*. In other
words, χ(x + x′) = χ(x)χ(x′) for all x,x′ G. A character χ is called unitary if
∣χ(x)∣ = 1 for all x
G. A character χ is called unitary if
∣χ(x)∣ = 1 for all x  G.
G.
If G is a finite abelian group, its Pontryagin dual is the set 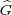 of its
characters. Under point-wise multiplication of characters,
of its
characters. Under point-wise multiplication of characters, 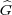 forms a group.
Once again, the binary operation is written additively, so that given
characters χ and χ′ of G, (χ + χ′)(x) = χ(x)χ′(x) for all x
forms a group.
Once again, the binary operation is written additively, so that given
characters χ and χ′ of G, (χ + χ′)(x) = χ(x)χ′(x) for all x  G. This is a
special case of a general construction for locally compact abelian
groups.
G. This is a
special case of a general construction for locally compact abelian
groups.
Proof. The proof is a sequence of exercises:
Exercise 1.5. Show that every finite abelian group is isomorphic to a product of finite cyclic groups.
It follows from the above proposition that 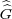
 G. However, in this case,
there is a canonical isomorphism G →
G. However, in this case,
there is a canonical isomorphism G →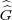 given by g
given by g ǧ where ǧ is defined
by
ǧ where ǧ is defined
by
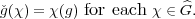
Let H be a subgroup of G. Given a representation (π,V ) of H, the representation of G induced from π is the representation (πG,V G) where
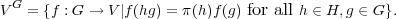
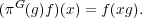
Now suppose that (τ,U) is a representation of G and (π,V ) is a
representation of H. Because H ⊂ G, we can regard U as a representation
of H by restricting the homomorphism G → GL(U) to H. Denote
this representation by τH. Given φ  HomG(τ,πG), define
HomG(τ,πG), define 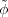 : U → V
by
: U → V
by
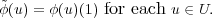
Theorem (Frobenius reciprocity). The map φ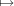
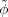 induces an
isomorphism
induces an
isomorphism
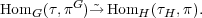
Proof. For ψ  HomH(τH,π) define
HomH(τH,π) define 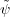 : U → V G by
: U → V G by
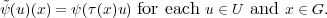
Therefore the maps φ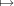
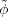 and ψ
and ψ
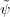 are mutual inverses. □
are mutual inverses. □
In this section we describe the homomorphisms between two induced representations. Let G be a finite group. Let H1 and H2 be subgroups. Let (π1,V 1) and (π2,V 2) be representations of H1 and H2 respectively. For f : G → V 1, and Δ : G → HomC(V 1,V 2), define a convolution Δ * f : G → V 2 by
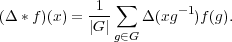
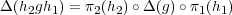
 H1, h2
H1, h2  H2 and g
H2 and g  G.
G.
Exercise 1.11. Show that the map LΔ : V 1G → V 2G defined by
f1 Δ * f1 is a homomorphism of G-modules.
Δ * f1 is a homomorphism of G-modules.
Proof. We construct an inverse mapping HomG(V 1G,V 2G) → D. For
this, let us define a collection fg,v of elements in V 1G indexed by g  G and
v
G and
v  V 1:
V 1:
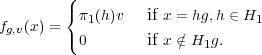
The above equation can be turned around to define, for each
L : HomG(V 1G,V 2G) a function Δ  D.
D.
Exercise 1.14. Show that if L  HomG(V 1,V 2), then the function
Δ : G → HomC(V 1,V 2) defined by
HomG(V 1,V 2), then the function
Δ : G → HomC(V 1,V 2) defined by
![ΔL(g)(v) = [G : H1]L(fg-1,v)(1)](notes37x.png)
Let G be a finite group, H a subgroup and (π,V ) a representation of H. The space V G can be decomposed into a direct sum

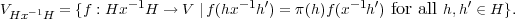
We have proved
Proposition 1.17. Let G be a finite group and H any subgroup. For every representation π of H, there is a canonical isomorphism of representations of H
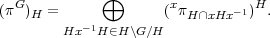
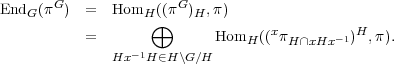
Theorem (Mackey’s irreducibility criterion). Let G be a finite
group and H a subgroup. Let π be an irreducible representation of H.
Then πG is irreducible if and only if, for any x H, the representations
π and (xπH∩xHx-1)H are disjoint.
H, the representations
π and (xπH∩xHx-1)H are disjoint.
Corollary 1.18. Suppose that G is a finite group and H a
normal subgroup. Then for any irreducible representation π of H, πG is
irreducible if and only if for every x H, xπ is not isomorphic to π.
H, xπ is not isomorphic to π.
The little groups method was first used by Wigner [Wig39], and
generalized by Mackey [Mac58] to construct representations of a group
from those of a normal subgroup. We will restrict ourselves to the case
where G is a finite group and N is a normal subgroup of G which is abelian.
Let 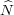 denote the Pontryagin dual of N (Section 1.2). Define an action of G
on
denote the Pontryagin dual of N (Section 1.2). Define an action of G
on 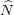 by
by
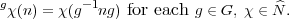

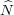 , write
, write
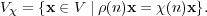
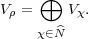
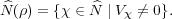
Proof. Suppose x  V χ, and g
V χ, and g  G. Then
G. Then
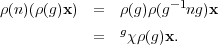
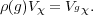 | (1.1) |
It follows that ⊕g GV gχ is invariant under ρ. From the irreducibility of ρ one
concludes that if V χ
GV gχ is invariant under ρ. From the irreducibility of ρ one
concludes that if V χ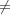 0, then ⊕g
0, then ⊕g GV gχ = V ρ. □
GV gχ = V ρ. □
For χ 
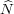 (ρ), let
(ρ), let
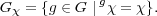
 Gχ, ρ(g) preserves V χ. Therefore, ρ
gives rise to a representation ρχ of Gχ on V χ.
Gχ, ρ(g) preserves V χ. Therefore, ρ
gives rise to a representation ρχ of Gχ on V χ.
Proof.

 V ρ, there is a unique decomposition
V ρ, there is a unique decomposition
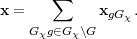
 V χ. The representation space of ρχG is
V χ. The representation space of ρχG is
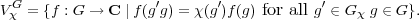
 G.
□
G.
□