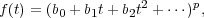Mn(F),
for every vector x
Mn(F),
for every vector x  Fn and every polynomial f(t)
Fn and every polynomial f(t)  F[t] define fx = f(A)x.
This endows Fn with the structure of an F[t]-module, which will be denoted
by MA.
F[t] define fx = f(A)x.
This endows Fn with the structure of an F[t]-module, which will be denoted
by MA.
Let F be any field.
Definition A.1. Two matrices A and B with entries in F are said to be similar if there exists an invertible matrix X such that BX = XA.
Similarity is an equivalence relation on the set of all n×n matrices. The
equivalence classes are called similarity classes. Given a matrix A  Mn(F),
for every vector x
Mn(F),
for every vector x  Fn and every polynomial f(t)
Fn and every polynomial f(t)  F[t] define fx = f(A)x.
This endows Fn with the structure of an F[t]-module, which will be denoted
by MA.
F[t] define fx = f(A)x.
This endows Fn with the structure of an F[t]-module, which will be denoted
by MA.
Conversely, given an F[t]-module M, pick any basis of M as an F-vector space. Let AM be the matrix by which t acts on M with respect to this basis. A different basis of M would give rise to a matrix similar to AM. Therefore, M determines a similarity class of matrices.
Proposition A.3. A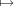 MA gives rise to a bijection between the
set of similarity classes of matrices and the set of isomorphism classes
of F[t]-modules.
MA gives rise to a bijection between the
set of similarity classes of matrices and the set of isomorphism classes
of F[t]-modules.
Definition A.4 (Simple matrix). Recall that an F[t]-module is called simple if there is no non-trivial proper subspace of M which is preserved by F[t]. A matrix A is said to be simple if MA is a simple F[t]-module.
Exercise A.6. For any two matrices A and B, let A⊕B denote the
block matrix  . A⊕B will be called the direct sum of A and B. Show
that MA⊕B = MA ⊕ MB (a canonical isomorphism of F[t]-modules).
. A⊕B will be called the direct sum of A and B. Show
that MA⊕B = MA ⊕ MB (a canonical isomorphism of F[t]-modules).
Definition A.7 (Indecomposable matrix). A matrix is said to be indecomposable if it is not similar to a matrix of the form A ⊕ B, where A and B are two strictly smaller matrices. Equivalently, A is indecomposable if MA is indecomposable as an F[t]-module.
Definition A.8 (Semisimple matrix). A matrix is said to be semisimple if it is similar to a direct sum of simple matrices. Equivalently, A is semisimple if MA is a semisimple F[t]-module (i.e., MA is a direct sum of simple F[t]-modules).
Exercise A.9. For any λ  F, show that the matrix
F, show that the matrix 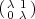 is
indecomposable, but not semisimple (and hence not simple either).
is
indecomposable, but not semisimple (and hence not simple either).
Let f(t) be any irreducible monic polynomial in F[t]. Given an F[t]-module M, its f-primary part is the submodule
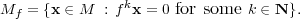
Theorem A.10 (Primary decomposition). [Jac84, Theorem 3.11] Let
M be an F[t]-module which is also a finite dimensional F-vector space.
Then Mf = 0 for all but finitely many irreducible monic polynomials
f(t)  F[t].
F[t].
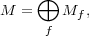
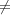 0.
0.
Let f  F[t] be an irreducible monic polynomial. An F[t]-module M is
called f-primary if M = Mf. M is called primary if it is f-primary for some
f.
F[t] be an irreducible monic polynomial. An F[t]-module M is
called f-primary if M = Mf. M is called primary if it is f-primary for some
f.
Exercise A.11. Let f(t)  F[t] be an irreducible monic polynomial,
and p(t)
F[t] be an irreducible monic polynomial,
and p(t)  F[t] be any monic polynomial. Show that F[t]∕p(t) is f-primary
if and only if p(t) = f(t)r for some r ≥ 0.
F[t] be any monic polynomial. Show that F[t]∕p(t) is f-primary
if and only if p(t) = f(t)r for some r ≥ 0.
Theorem A.12. Let f(t)  F[t] be an irreducible monic polynomial,
and A be a square matrix. Then MfA
F[t] be an irreducible monic polynomial,
and A be a square matrix. Then MfA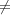 0 if and only if f(t) divides the
characteristic polynomial of A.
0 if and only if f(t) divides the
characteristic polynomial of A.
Proof. Let χA denote the characteristic polynomial of A. If f is an irreducible polynomial that does not divide χA, then there exist polynomials r and s such that fr+χAs = 1. Evaluating at A and applying the Cayley-Hamilton theorem shows that f(A)r(A) = I. It follows that f(A) is non-singular. Hence f(A)k is also non-singular for every positive integer k. Therefore, MfA = 0.
Conversely, if MfA = 0, then f(A)k is non-singular for every k  N. In
particular, f(A) is non-singular. Let E be a splitting field of f. Suppose
that
N. In
particular, f(A) is non-singular. Let E be a splitting field of f. Suppose
that
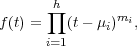
 E distinct, and m1,…,mh
E distinct, and m1,…,mh  N. Therefore,
N. Therefore,
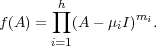
If MA is f-primary then the matrix A is called an f-primary matrix. It follows that a matrix is primary if and only if its characteristic polynomial has a unique irreducible factor.
Corollary A.13. Every matrix A  Mn(F) is similar to a matrix of
the form
Mn(F) is similar to a matrix of
the form
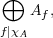
Thus, the study of similarity classes of matrices is reduced to the study of similarity classes of primary matrices.
Theorem A.14 (Structure theorem). [Jac84, Section 3.8] For every
F[t]-module M, there exist non-constant monic polynomials f1,…,fr such that
f1∣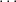 ∣fr and
∣fr and
![M ~= F[t]∕f (t)⊕ ⋅⋅⋅⊕ F[t]∕f (t).
1 r](notes411x.png)
Fix an irreducible monic polynomial f(t)  F[t]. If M is f-primary, then by
Exercise A.11, each for each i, fi = fλi for some λi > 0. Therefore,
F[t]. If M is f-primary, then by
Exercise A.11, each for each i, fi = fλi for some λi > 0. Therefore,
Corollary A.15 (Structure of a primary module). If M is an
f-primary F[t]-module, then there exists a non-decreasing sequence of
integers λ1 ≤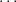 ≤ λr such that
≤ λr such that
![M ~= F [t]∕f(t)λ1 ⊕ ⋅⋅⋅⊕ F[t]∕f(t)λr.](notes413x.png)
Definition A.16 (Partition). A partition is a finite sequence
λ = (λ1,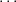 ,λr) of positive integers such that λ1 ≤
,λr) of positive integers such that λ1 ≤ 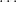 ≤ λr. Define
∣λ∣ := λ1 +
≤ λr. Define
∣λ∣ := λ1 + 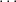 + λr. One says that λ is a partition of ∣λ∣. The length of λ
is the non-negative integer r (there is an ‘empty partition’ of length 0
denoted ∅, with ∣∅∣ = 0). Let Λ denote the set of all partitions.
+ λr. One says that λ is a partition of ∣λ∣. The length of λ
is the non-negative integer r (there is an ‘empty partition’ of length 0
denoted ∅, with ∣∅∣ = 0). Let Λ denote the set of all partitions.
Given a partition λ = (λ1,…,λl), define an F[t]-module
![λ1 λl
Mf,λ = F[t]∕f(t) ⊕ ⋅⋅⋅⊕ F[t]∕f(t) .](notes417x.png)
Exercise A.17. Suppose that f and f′ are two irreducible monic polynomials, λ and λ′ two partitions. Show that the F[t]-modules Mf,λ and Mf′,λ′ are isomorphic if and only if f = f′ and λ = λ′.
Let S denote the set of all irreducible monic polynomials in F[t]. Given a
function ψ : S → Λ such that ψ(f) = ∅ for all but finitely many f  S, let Mφ
denote the F[t]-module
S, let Mφ
denote the F[t]-module
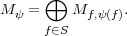
 Sdeg(f)∣ψ(f)∣. Let nψ = dimF Mψ.
Sdeg(f)∣ψ(f)∣. Let nψ = dimF Mψ.
Theorem A.18 (Similarity classes of matrices). The map ψ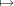 Mψ
is a bijective correspondence between the set of all functions S → Λ with
the property that ψ(f) = ∅ for all but finitely many f
Mψ
is a bijective correspondence between the set of all functions S → Λ with
the property that ψ(f) = ∅ for all but finitely many f  S and nψ = n
and the set of isomorphism classes of n-dimensional F[t]-modules (and
hence the set of similarity classes of n × n matrices).
S and nψ = n
and the set of isomorphism classes of n-dimensional F[t]-modules (and
hence the set of similarity classes of n × n matrices).
There is a version of the Jordan canonical form for matrices for which the irreducible factors of the characteristic polynomial have derivatives which are not identically zero.
In order to obtain this form, we need the following result:
Theorem A.19. Suppose that f an irreducible monic polynomial in F[t] such that f′(t) is not identically zero. Let E denote the field F[t]∕f(t). Then the rings k[t]∕f(t)r and E[u]∕ur are isomorphic.
Proof. The main step in the proof is a version of Hensel’s Lemma
Lemma A.20 (Hensel). There exists qr(t)  F[t] such that qr(t) ≡ t
mod f(t), and f(qr(t)) ≡ 0 mod f(t)r.
F[t] such that qr(t) ≡ t
mod f(t), and f(qr(t)) ≡ 0 mod f(t)r.
Proof. The proof is by induction on r. When r = 1, one may take q1(t) = t.
Suppose that qr-1(t)  F[t] is such that
F[t] is such that

 F[t],
F[t],
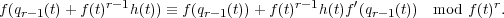
 F[t] such that f′r + fs = 1, which means that f′(t)r(t) ≡ 1
mod f(t). Since f(qr-1(t)) ≡ 0 mod f(t)r-1, there exists f1(t)
F[t] such that f′r + fs = 1, which means that f′(t)r(t) ≡ 1
mod f(t). Since f(qr-1(t)) ≡ 0 mod f(t)r-1, there exists f1(t)  F[t] such
that
F[t] such
that
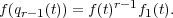
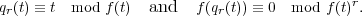
Given qr(t) as in Hensel’s lemma, the map
![φ : F[u,v]∕(f(v),ur) → F[t]∕f(t)r](notes424x.png)
Definition A.21 (Companion matrix). Let f(t) = tn-an-1tn-1 -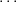 -a1t-a0.
Then the companion matrix of f is the n × n matrix:
-a1t-a0.
Then the companion matrix of f is the n × n matrix:
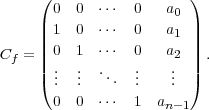
Theorem A.22 (Block Jordan Canonical Form). Let A  Mn(F) be
such that for every irreducible factor f of the characteristic polynomial of A,
f′ is not identically zero. Then A can be written as a block diagonal matrix
with blocks of the form
Mn(F) be
such that for every irreducible factor f of the characteristic polynomial of A,
f′ is not identically zero. Then A can be written as a block diagonal matrix
with blocks of the form
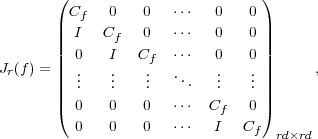
Proof. By Exercise A.6 and Theorem A.10 one may assume that A is f-primary, for some irreducible monic polynomial f. Let E = F[v]∕f(v). By Corollary A.15 and Theorem A.15, there exists a partition λ such that
![A ~ λ1 λr
M = E[u]∕u ⊕ ⋅⋅⋅⊕ E[u]∕u .](notes428x.png)
 (f(t)). But θ(t)
(f(t)). But θ(t) (f(t)2), for if it did, we
would have
(f(t)2), for if it did, we
would have 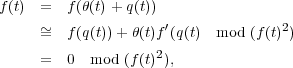
![r r r
F[t]∕(f(t) ) → E[u]∕u = F[u,v]∕(u ,f(v)),](notes431x.png)
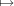 αu + v. Since A acts by t, with respect to the basis of E[u]∕uλi over F
given by
αu + v. Since A acts by t, with respect to the basis of E[u]∕uλi over F
given by
The hypothesis on A in Theorem A.22 always holds when F is a perfect field, as we shall see in Section A.6. By Corollary B.8 every finite field is perfect. Therefore, every matrix over a finite field has a Jordan canonical form.
For any A  Mn(F) define
Mn(F) define
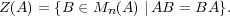
Theorem A.23. Let A  Mn(F) be a matrix such that for each
irreducible factor f of the characteristic polynomial of A, f′ is not
identically zero. Suppose that A is similar to ⊕fAf, where Af is f-primary
(see Corollary A.13). Then Z(A)
Mn(F) be a matrix such that for each
irreducible factor f of the characteristic polynomial of A, f′ is not
identically zero. Suppose that A is similar to ⊕fAf, where Af is f-primary
(see Corollary A.13). Then Z(A) ⊕fZ(Af). If A is f-primary, E = F[t]∕f(t),
and λ is the partition associated to MA in Corollary A.15, then
⊕fZ(Af). If A is f-primary, E = F[t]∕f(t),
and λ is the partition associated to MA in Corollary A.15, then
.](notes436x.png)
Note that the group of units of the centraliser algebra Z(A) will be the centraliser of A in GLn(F).
Proof. The theorem follows easily from Theorem A.19, using the
fact that EndF[t]MA Z(A). □
Z(A). □
Definition A.24. A perfect field is either a field of characteristic
zero, or a field of characteristic p > 0 for which the map x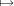 xp is
bijective.
xp is
bijective.
Theorem A.25. Suppose that F is a perfect field and f(t)  F[t]
is a non-constant irreducible polynomial. Then f′(t) does not vanish
identically.
F[t]
is a non-constant irreducible polynomial. Then f′(t) does not vanish
identically.
Proof. If f′ = 0, then the characteristic of F must be p > 0 and f must be of the form
 E such that bip = ai. Then
E such that bip = ai. Then