Scholium 5
Let
f :
Sn Sn
Sn be any continuous map of degree
d, where
n > 1.
Then the induced map
is
- (v)
- multiplication by d if i < 2n - 1
- (vi)
- multiplication by d on the torsion subgroup, for i = 2n - 1
(and in particular on
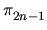 , if n is odd)
, if n is odd)
- (vii)
- multiplication by d2 on
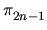 (Sn)
(Sn) 
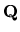 .
.
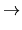
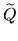
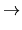 Sn + 1.
Sn + 1. (*)
(*)