1.1 Cell structure

We begin by recalling the cell decomposition of a quadric hypersurface in a form convenient for us. We will proceed by induction on dimension. The two smallest dimensions are :

n = 1:

Q is $\mbox{$\bf P$}$¹ $\hookrightarrow$ $\mbox{$\bf P$}$² as a conic and has a natural cell decomposition Q = $\mbox{$\bf C$}$ $\cup$ {$\infty$}. We have for d $\in$ $\mbox{$\bf N$}$ maps F_d : Q$\to$Q ( z $\mapsto$ z^d) preserving the cell structure.

n = 2:

Q is $\mbox{$\bf P$}$¹×$\mbox{$\bf P$}$¹ $\hookrightarrow$ $\mbox{$\bf P$}$² via the Segre embedding and has a natural cell decomposition

Q = ($$\mbox{$\bf C$}$$×$$\mbox{$\bf C$}$$) $$\cup$$ ($$\mbox{$\bf C$}$$×{$$\infty$$}) $$\cup$$ ({$$\infty$$}×$$\mbox{$\bf C$}$$) $$\cup$$ {($$\infty$$,$$\infty$$)}.

For all d $\in$ $\mbox{$\bf N$}$, we have maps F_d : Q$\to$Q ( (z, w) $\mapsto$ (z^d, w^d)) which preserve the cell structure.

We henceforth assume that n $\geq$ 3.

Scholium 1   Q has a cell decomposition with cells in each even (real) dimension (the Bruhat cell decomposition) such that we have:

1. For n $\geq$ 3, Q^{(2n - 2)} = C is the projective cone over Q' $\subset$ $\mbox{$\bf P$}$^{n - 1}, a smooth quadric hypersurface of complex dimension n - 2.
2. There is exactly one cell in each even (real) dimension except in dimension n for n = 2k.
3. Q⁽ⁿ⁾ may be explicitly described as follows:

   n = 2k:

   Q⁽ⁿ⁾ = L' $\cup$ L'', where L', L'' $\cong$ $\mbox{$\bf P$}$^k are linear subspaces of $\mbox{$\bf P$}$^{n + 1} and L' $\cap$ L'' = L $\cong$ $\mbox{$\bf P$}$^{k - 1}.

   n = 2k + 1:

   Q⁽ⁿ⁾ = L $\cong$ $\mbox{$\bf P$}$^k is a linear subspace of $\mbox{$\bf P$}$^{n + 1}.

4. For n $\geq$ 3, Q^{(n + 2)} $\subset$ C is the Thom space over Q'⁽ⁿ⁾ of the complex line bundle $\mbox{${\cal O}_{Q'^{(n)}}$}$(1).

Proof:     Let p be any point of Q and let H $\subset$ $\mbox{$\bf P$}$^{n + 1} be a hyperplane tangent to Q at p. Then Q $\cap$ H = C is the projective cone over Q' $\subset$ $\mbox{$\bf P$}$^{n - 1}, a smooth quadric hypersurface of complex dimension n - 2 (i.e. C is the Thom space of the complex line bundle $\mbox{${\cal O}_{Q'}$}$(1) = $\mbox{${\cal O}_{\P^{n-1}}$}$(1)$\mid_{Q'}^{}$). By induction on dimension we get a cell decomposition of Q'. If Q'^(m) is the m-skeleton of Q', and C(Q'^(m)) is the Thom space of $\mbox{${\cal O}_{Q'^{(m)}}$}$(1), then C(Q'^(m)) - C(Q'^{(m - 1)}) is a union of cells of dimension m + 2. Thus, we obtain a cell decomposition of C. Since Q - C = $\mbox{$\bf C$}$ⁿ, we obtain the desired cell structure. $\Box$
We shall use the following construction. Construction 1 Let X, Y be compact topological spaces, L and M complex line bundles on X and Y respectively. Let f : X$\to$Y be a continuous map, such that there is an isomorphism $\varphi$ : L^{$\otimes$ d}$\to$f^*(M), for some positive integer d. Then there exists a map $\Phi$ : L$\to$M giving a commutative diagram

L	$$\;\stackrel{\Phi}{\longrightarrow}\;$$	M
$$\downarrow$$		$$\downarrow$$
X	$$\;\stackrel{f}{\longrightarrow}\;$$	Y

where $\Phi$ is the d-th power map on fibres of the vertical arrows. The restriction of $\Phi$ to the S¹-bundles $\widetilde{X}$, $\widetilde{Y}$ of L, M respectively induces a map $\widetilde{f}$ : $\widetilde{X}$$\to$$\widetilde{Y}$, which has degree d along the fibres. If C(X, L) and C(Y, M) denote the Thom spaces of L and M respectively, we have a map C(f )= C(f,$\varphi$) : C(X, L)$\to$C(Y, M) induced by $\Phi$.

In particular, if X $\subset$ $\mbox{$\bf P$}$^N is a projective variety, f : X$\to$X an algebraic self-map, L = M = $\mbox{${\cal O}_{X}$}$(1), and $\varphi$ is an isomorphism of algebraic line bundles, then C(X, L) is the projective cone (in $\mbox{$\bf P$}$^{N + 1}) of X and C(f ) can be regarded as an algebraic self-map of C(X, L). Note that $\varphi$ is unique upto a scalar multiple. We had noted the existence of morphisms F_d : Q$\to$Q for each d > 0, for a smooth quadric Q of dimension one or two. These maps satisfy F_d1oF_d2 = F_d1d2 for all d₁, d₂ > 0. By repeatedly applying the above constructions, we obtain

Lemma 2   For each d > 0, there is an algebraic morphism

F_{d, n} : Q^{(n + 2)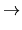}$$\to$$Q^{(n + 2)}

and an algebraic isomorphism

$$\varphi_{d,n}^{}$$ : $$\mbox{${\cal O}_{Q^{(n+2)}}$}$$(d )$$\to$$F_{d, n}^*($$\mbox{${\cal O}_{Q^{(n+2)}}$}$$(1))

such that

(i)

under the identification (by Scholium 1)

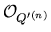
Q^{(n + 2)} = C(Q'⁽ⁿ⁾,$$\mbox{${\cal O}_{Q'^{(n)}}$}$$(1))

we have

F_{d, n} = C(F_{d, n - 2},$$\varphi_{d,n-2}^{}$$)

.

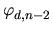
(ii)

F_{d1, n}oF_{d2, n} = F_{d1d2, n}.

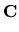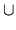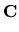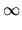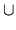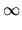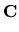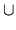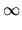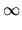$\Box$

If F_{d, n - 2} : Q'⁽ⁿ⁾$\to$Q'⁽ⁿ⁾ extends to a continuous map f' : Q'$\to$Q', then the isomorphism $\varphi_{d,n-2}^{}$ can be extended to an isomorphism (of topological complex line bundles)

$$\varphi{^\prime}$$ : $$\mbox{${\cal O}_{Q'}$}$$(d )$$\to$$f'^*($$\mbox{${\cal O}_{Q'}$}$$(1)).

Then the induced continuous map C(f') = C(f',$\varphi{^\prime}$) : C$\to$C restricts to F_{d, n} on Q^{(n + 2)} $\subset$ C. Since Q is obtained from C by attaching $\mbox{$\bf C$}$ⁿ via a map a : S^{2n - 1}$\to$C, the map C(f') : C$\to$C extends to a map f : Q$\to$Q if and only if C(f')_*([a]) = m[a] $\in$ $\pi_{2n-1}^{}$(C), for some m $\in$ $\mbox{$\bf Z$}$. Thus, we need to compute $\pi_{2n-1}^{}$(C), and the action of C(f')_* on it.