Research

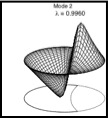
I use methods of continuum mechanics (elasticity theory, fluid dynamics) and statistical mechanics (classical field theory, generalised hydrodynamics, stochastic differential equations) to model the statics and dynamics of soft materials.

Typically, the mathematical models have no analytical solutions and numerical methods must be used to solve them. I use a combination of Monte Carlo, molecular dynamics, finite difference and lattice Boltzmann methods to explore the physics contained in the models. Scientific visualisation is one way of drawing insight from the numbers generated by the numerics. Realistic models often involve millions of degrees of freedom, necessitating the use of supercomputers and parallel computing.

Probability theory, which is the basis of all of statistical mechanics, finds use in quantitative models of biological, economic and social phenomena. Often, there is a striking similarity in the mathematical models which describe completely different phenomena. I find it interesting to explore these commonalities.

Click on the links below to see some of my representative research.