4. The Iso-spectral problem

An algebraic construction for the KP Hierarchy can be given analogous to the “exp” map for Drinf’eld modules. The infinite Grassmannian is described as follows:

Let X be any variety and p a smooth point on it. This gives us a base point n ⋅ p in Symⁿ(X), the n-fold symmetric product of X with itself. We then have natural base point preserving maps Symⁿ(X) → Sym^n+k(X) obtained by adding the zero-cycle k ⋅ p. The direct limit

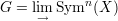
has a natural multiplication induced by the morphisms

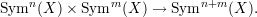
If X is 1-dimensional this group G acts on 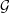and the flow associated with this action is then the KP flow.