Theorem 7.1 (S. Lefschetz). Let Y be a smooth complete intersection
subvariety of a smooth projective variety X. Then 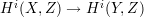 is an isomorphism for i < dimY and an injection for i = dimY .
is an isomorphism for i < dimY and an injection for i = dimY .
Along with V. Srinivas the papers of U. Morin [17] and A. Predonzan [19] were resurrected. In these papers it is shown that a general complete intersection of sufficiently small multidegree is unirational. The method of proof suggested that some further “rational”-like properties could be shown for these varieties.
Recent work of M. V. Nori [18] regarding cohomological connectivity of hypersurfaces generalises earlier results of S. Lefschetz, P. Griffiths, and others. In a slightly different direction cohomological connectivity results for hypersurfaces of low degree have been shown by H. Esnault, M. V. Nori and V. Srinivas [7].
The above two pieces of work tie up with the conjectures of S. Bloch and A. A. Beilinson to suggest some conjectures on the geometry of hypersurfaces and complete intersections in Pn. We formulate and prove some cases of these conjectures.
The first cohomological result is
Theorem 7.1 (S. Lefschetz). Let Y be a smooth complete intersection
subvariety of a smooth projective variety X. Then 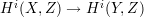 is an isomorphism for i < dimY and an injection for i = dimY .
is an isomorphism for i < dimY and an injection for i = dimY .
The corresponding conjecture is
Conjecture 7.2 (R. Hartshorne). Let X be a smooth projective variety
and Y a complete intersection subvariety, then 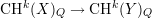 is
an isomorphism for k < dimY∕2.
is
an isomorphism for k < dimY∕2.
We prove a special case this conjecture when X = Pn, in a weakened form
Theorem 7.3. Given a sequence of positive integers d1,…,dr and a
non-negative integer l. Let Y be a smooth subvariety of Pn of multidegree
(d1,…,dr). If n is sufficiently large then 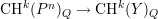 is an
isomorphism for k ≤ l.
is an
isomorphism for k ≤ l.
The second cohomological result
Theorem 7.4 (H. Esnault, M. V. Nori, V. Srinivas). Let X be the zero
locus of a collection of homogeneous equations fi of degree di, where d1 ≤
 ≤ dr. Then for any i ≥ 0 we have
≤ dr. Then for any i ≥ 0 we have 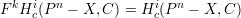 where F⋅ denotes the Hodge filtration and
where F⋅ denotes the Hodge filtration and
![[ ∑ ]
n-----rj=2dr-
k = d1 .](work_done27x.png)
leads to the following
Conjecture 7.5. Let X be a smooth subvariety of Pn of multidegree d1 ≤
 ≤ dr, the CHp(X)Q = Q for p < k, with k as above.
≤ dr, the CHp(X)Q = Q for p < k, with k as above.
We prove a weakened form of this conjecture which generalises earlier results of A. A. Roitman [20]
Theorem 7.6. Given a sequence of positive integers d1,…,dr and a
non-negative integer l. Let X be a subscheme of Pn of multidegree (d1,…,dr).
If n is sufficiently large then 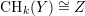 for k ≤ l and this group is
generated by the class of a linear space Pl ⊂ X.
for k ≤ l and this group is
generated by the class of a linear space Pl ⊂ X.
The proof for 7.3 uses 7.6 and a generalization of a result of S. Bloch and V. Srinivas [2].