


Next: Integration
Up: New Functions from old
Previous: Inverse functions
We will prove the implicit function theorem.
Let f (x, y) be a continuous function of two variables so that it is
continuous, and differentiable with respect to y when x is kept
fixed; in particular, we have expression
f (x, y) = f0(x, y0) + f1(x, y0)(y - y0) + ox(y - y0)
where the subscript in the ox denotes the dependence of the
condition on x. The function f1(x, y) is denoted by
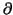 f /
f /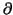 y and is called the partial derivative of f with respect
to y (we have already seen this for the case of polynomials). We
further assume that f1 is continuous.
y and is called the partial derivative of f with respect
to y (we have already seen this for the case of polynomials). We
further assume that f1 is continuous.
Figure 7:
The implicit function
|
|
Now suppose that f (a, b) = 0 and
c = (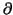 f /
f /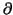 y)(a, b)
y)(a, b)  0. We want to find the implicit function h(x) defined by f = 0
(see 7). We do this by showing that for each x near a
there is a unique y so that f (x, y) = 0. Equivalently, we need to
show that the function
g(x, y) = y - f (x, y)/c has a unique fixed point
for any chosen x near a.
0. We want to find the implicit function h(x) defined by f = 0
(see 7). We do this by showing that for each x near a
there is a unique y so that f (x, y) = 0. Equivalently, we need to
show that the function
g(x, y) = y - f (x, y)/c has a unique fixed point
for any chosen x near a.
Contractions give rise to functions with a unique fixed point.
Exercise 49
Let 0 < c < 1 be a constant. Let g(x) be a function so that g
send the interval [a, b] to itself and
| g(x) - g(y)| < c| x - y|
for all x and y in [a, b]. Show that
g(x0) = x0 for exactly
one point x0 in [a, b].
Consider the function
g(x, y) = y - f (x, y)/c as above; we have
g(a, b) = b and
(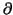 g/
g/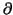 y) = 0. For each fixed x we
would like g(x, y) to be a contraction on some interval around
b. As a first step:
y) = 0. For each fixed x we
would like g(x, y) to be a contraction on some interval around
b. As a first step:
Exercise 50
Using the continuity of
f1 show that there is an interval
[
a -
r,
a +
r] around
a and an interval [
b -
s,
b +
s] around
b so
that
|(
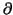 g
g/
 y
y)(
x,
y)|
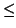
1/2 for
x and
y in
these respective intervals. (Hint: Write
 g
g/
 y
y in
terms of
f1 to show that it is continuous). In particular, by the
mean value theorem show that
|
g(
x,
y) -
g(
x,
y')|
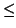
1/2(
y -
y') on these intervals.
Now by the continuity of f (and thus of g) we can choose a smaller
r so that
| g(x, b) - g(a, b)| 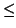 s/2 for x in the interval
[a - r, a + r]. Since g(a, b) = b, it follows that
g(x, y) = b + (g(x, y) - g(x, b)) + (g(x, b) - g(a, b)) lies in the interval
[b - s, b + s]. Applying the above exercise it follows that for every x
there is a unique point y so that g(x, y) = y or equivalently
f (x, y) = 0. We denote this point y as h(x). This function h is
the required implicit function.
s/2 for x in the interval
[a - r, a + r]. Since g(a, b) = b, it follows that
g(x, y) = b + (g(x, y) - g(x, b)) + (g(x, b) - g(a, b)) lies in the interval
[b - s, b + s]. Applying the above exercise it follows that for every x
there is a unique point y so that g(x, y) = y or equivalently
f (x, y) = 0. We denote this point y as h(x). This function h is
the required implicit function.
We have the identity,
Applying the mean value theorem to g(x', y) we obtain
|
h(
x) -
h(
x')|
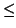
|
g(
x,
h(
x)) -
g(
x',
h(
x)| +
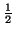
|
h(
x) -
h(
x')|
Exercise 51
Use the above inequality and the continuity of g(x, y0)
for every fixed y0 to conclude the h(x) is continuous.
Now if we assume in addition that f is differentiable to order k
then it follows that h is also differentiable to order k by an
entirely similar reasoning to the one in the above exercise.
Exercise 52
If
f (
x,
y) has the form (near the point (
a,
b))
with
f0, 1 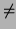
0, then show that the implicit function
g(
x)
has the form (near
x =
a),
g(
x) =
b -
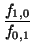
(
x -
a) +
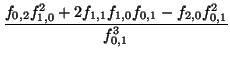
(
x -
a)
2 +
o((
x -
a)
2)



Next: Integration
Up: New Functions from old
Previous: Inverse functions
Kapil H. Paranjape
2001-01-20
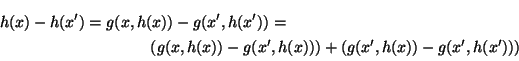
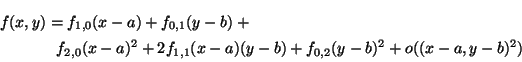
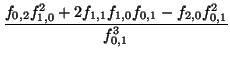 (x - a)2 + o((x - a)2)
(x - a)2 + o((x - a)2)