


Next: 3 Divisors on varieties
Up: Algebraic Cycles
Previous: 1 Model case of
Let X be a non-singular variety over k. An algebraic cycle of codimension p is an element of the free Abelian
group on irreducible subvarieties of X of codimension p; the group of
these cycles is denoted Zp(X). As in the case of curves one can
introduce the effective cycles
Zp(X) 0 which is the
sub-semigroup of Zp(X) consisting of non-negative linear
combinations. There is a subgroup
Rp(X)
0 which is the
sub-semigroup of Zp(X) consisting of non-negative linear
combinations. There is a subgroup
Rp(X) 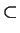 Zp(X), defined to be the subgroup generated by all the cycles
div(f )W where W ranges over irreducible subvarieties of codimension
p - 1 in X, and
f
Zp(X), defined to be the subgroup generated by all the cycles
div(f )W where W ranges over irreducible subvarieties of codimension
p - 1 in X, and
f 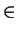 k(W)*. The quotient
k(W)*. The quotient
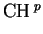 (X) = Zp(X)/Rp(X) is
called the Chow group of codimension p cycles on X modulo
rational equivalence; if n = dim X then we use the notation
(X) = Zp(X)/Rp(X) is
called the Chow group of codimension p cycles on X modulo
rational equivalence; if n = dim X then we use the notation
 (X) =
(X) =  (X). For p = 1 and X a smooth projective curve the Chow
group
(X). For p = 1 and X a smooth projective curve the Chow
group 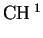 (X) is precisely the class group
(X) is precisely the class group 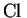 (X) introduced above.
(X) introduced above.
The generalisation of Schubert calculus on the Grassmannians
is the intersection product
making
 (X) =
(X) = 
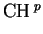 (X) into an associative, commutative, graded ring,
where
(X) into an associative, commutative, graded ring,
where
 (X) =
(X) =  Z, and
Z, and
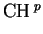 (X) = 0 for p > dim X.
The Chow ring is thus an algebraic analogue for the even cohomology ring
(X) = 0 for p > dim X.
The Chow ring is thus an algebraic analogue for the even cohomology ring

 (X,
(X, Z) in topology. A refined version of
this analogy is examined in Section 6. In any case we note the following
`cohomology-like' properties.
Z) in topology. A refined version of
this analogy is examined in Section 6. In any case we note the following
`cohomology-like' properties.
-
X


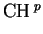 (X) is a contravariant functor from the
category of smooth varieties over k to graded rings.
(X) is a contravariant functor from the
category of smooth varieties over k to graded rings.
- If X is projective and n = dim X, there is a well defined
degree homomorphism
deg :
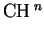 (X)
(X)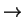
 Z
given by
deg(
Z
given by
deg(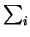 niPi) =
niPi) = 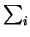 ni. This allows one to define
intersection numbers of cycles of complementary dimension, in a purely
algebraic way, which agree with those defined via topology when
k =
ni. This allows one to define
intersection numbers of cycles of complementary dimension, in a purely
algebraic way, which agree with those defined via topology when
k =  C (see
item 7 below).
C (see
item 7 below).
- If f : X
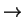 Y is a proper morphism of smooth varieties, there are
`Gysin' maps
f* :
Y is a proper morphism of smooth varieties, there are
`Gysin' maps
f* : 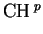 (X)
(X)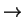
 (Y) for all p, where
d = dim Y - dim X; here if p + d < 0, we define f* to be 0; the induced map
(Y) for all p, where
d = dim Y - dim X; here if p + d < 0, we define f* to be 0; the induced map

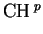 (X)
(X)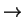

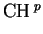 (Y) is
(Y) is

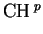 (Y)-linear
(`projection formula').
(Y)-linear
(`projection formula').
-
f* :
 (X)
(X)
 (V) for any vector bundle f : V
(V) for any vector bundle f : V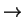 X.
X.
- If V is a vector bundle (i.e., locally free sheaf) of rank r,
then there are Chern classes
cp(V)
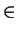
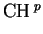 (X), such that
(X), such that
- c0(V) = 1,
- cp(V) = 0 for p > r, and
- for any exact sequence
we have
c(V2) = c(V1)c(V3), where
c(Ei) =
 cp(Vi) are
the total Chern classes.
cp(Vi) are
the total Chern classes.
Moreover, we also have the following property.
- If
f :
 P(V)
P(V)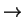 X is the projective bundle associated to a vector
bundle of rank r,
X is the projective bundle associated to a vector
bundle of rank r,
 (
( P(V)) is a
P(V)) is a  (X)-algebra generated
by
(X)-algebra generated
by
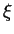 = c1(
= c1(
 P(V)(1)), the first Chern class of the tautological
line bundle, which is subject to the relation
P(V)(1)), the first Chern class of the tautological
line bundle, which is subject to the relation

-
c1(
V)

+
... + (- 1)
rcn(
V) = 0
- If
k =
 C, there are cycle class homomorphisms
C, there are cycle class homomorphisms
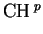 (X)
(X)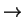
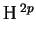 (X,
(X, Z) such that the intersection product
corresponds to the cup product in cohomology, and for a vector bundle E,
the cycle class of cp(E) is the topological p-th Chern class of E.
Z) such that the intersection product
corresponds to the cup product in cohomology, and for a vector bundle E,
the cycle class of cp(E) is the topological p-th Chern class of E.
In analogy with the case of curves we have that
c1 : 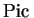 (X)
(X)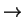
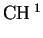 (X) is an isomorphism. In fact more is true.
If K0(X) is the Grothendieck ring of vector bundles on X, the
Chern character (defined using Chern classes by the same formula as
in topology) gives a ring isomorphism
(X) is an isomorphism. In fact more is true.
If K0(X) is the Grothendieck ring of vector bundles on X, the
Chern character (defined using Chern classes by the same formula as
in topology) gives a ring isomorphism
Identifying the group K0(X) with the Grothendieck group G0(X) of
coherent sheaves, we may extend the definitions of Chern classes and Chern
character to coherent sheaves; now the Grothendieck-Riemann-Roch
theorem states that for any proper morphism f : X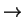 Y, and any coherent
sheaf
Y, and any coherent
sheaf  on X, we have
on X, we have
f*(
ch(

)
td (
X)) =
ch(
f!
)
td (
Y),
where
td (X) 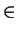
 (X),
td (Y)
(X),
td (Y) 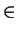
 (Y) are the Todd classes of
the tangent sheaves of X and Y respectively; here
f! : G0(X)
(Y) are the Todd classes of
the tangent sheaves of X and Y respectively; here
f! : G0(X)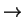 G0(Y) is
f!(
G0(Y) is
f!( ) =
) =  (- 1)i[Rif*
(- 1)i[Rif* ], and the Todd
class of a coherent sheaf is a certain polynomail in its Chern classes. If
X is proper over k (e.g., X is projective) of dimension n,
and Y is a point, this gives a formula (the
Grothendieck-Hirzebruch-Riemann-Roch formula)
], and the Todd
class of a coherent sheaf is a certain polynomail in its Chern classes. If
X is proper over k (e.g., X is projective) of dimension n,
and Y is a point, this gives a formula (the
Grothendieck-Hirzebruch-Riemann-Roch formula)

(
X,

) =

(- 1)
idim
k
(
X,

) = deg
 ch
ch(

)
td (
X)

,
where the
subscript n means that we compute the degree of the component in
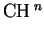 (X). For further details, see [14], Chapter 15.
(X). For further details, see [14], Chapter 15.



Next: 3 Divisors on varieties
Up: Algebraic Cycles
Previous: 1 Model case of
Kapil Hari Paranjape
2002-11-21
![]() 0 which is the
sub-semigroup of Zp(X) consisting of non-negative linear
combinations. There is a subgroup
Rp(X)
0 which is the
sub-semigroup of Zp(X) consisting of non-negative linear
combinations. There is a subgroup
Rp(X) ![]() Zp(X), defined to be the subgroup generated by all the cycles
div(f )W where W ranges over irreducible subvarieties of codimension
p - 1 in X, and
f
Zp(X), defined to be the subgroup generated by all the cycles
div(f )W where W ranges over irreducible subvarieties of codimension
p - 1 in X, and
f ![]() k(W)*. The quotient
k(W)*. The quotient
![]() (X) = Zp(X)/Rp(X) is
called the Chow group of codimension p cycles on X modulo
rational equivalence; if n = dim X then we use the notation
(X) = Zp(X)/Rp(X) is
called the Chow group of codimension p cycles on X modulo
rational equivalence; if n = dim X then we use the notation
![]() (X) =
(X) = ![]() (X). For p = 1 and X a smooth projective curve the Chow
group
(X). For p = 1 and X a smooth projective curve the Chow
group ![]() (X) is precisely the class group
(X) is precisely the class group ![]() (X) introduced above.
(X) introduced above.
![]() (X)
(X)![]()
![]() (X) is an isomorphism. In fact more is true.
If K0(X) is the Grothendieck ring of vector bundles on X, the
Chern character (defined using Chern classes by the same formula as
in topology) gives a ring isomorphism
(X) is an isomorphism. In fact more is true.
If K0(X) is the Grothendieck ring of vector bundles on X, the
Chern character (defined using Chern classes by the same formula as
in topology) gives a ring isomorphism