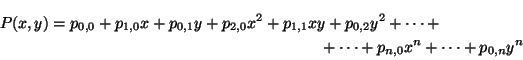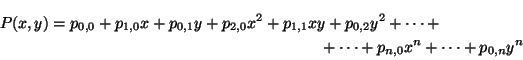Next: Sequences
Up: Polynomials and polynomial functions
Previous: Polynomials in one variable
Let us begin by considering polynomials in two variables x and y
where pk, l are constants. The degree of a term
pk, lxkyl
is defined as k + l if pk, l is non-zero. The degree of a
polynomial is the maximum of the degrees of each of its non-zero terms
and the degree of the zero polynomial is undefined as before.
Exercise 22
Define the arithmetic operations on polynomials algorithmically so
that polynomial manipulations can be implemented on a computer.
Polynomials can be ``evaluated'' to give functions; for any choice of
a pair of constants (a, b), we can substitute x by a and y by
b to obtain the ``value'' of the polynomial. By identifying the
pair of constants (a, b) with the corresponding point in the plane,
this gives us the function (on the plane) associated with the
polynomial. The points where the function associated with the
polynomial vanishes are called solutions of the polynomial.
In particular, a polynomial P(x, y) as above has the origin (0, 0)
as a solution only if the constant term p0, 0 is zero. More
generally, we say a polynomial vanishes to order m at the origin
(0, 0) if all its terms have degree at least m.
The Binomial theorem allows us to extend this notion to points
(a, b) other than the origin.
Exercise 23
Use the Binomial theorem to write a polynomial of degree
n as a
sum of terms of the form
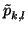
(
x -
a)
k(
y -
b)
l
where
k +
l is at most
n.
Thus we can say that a polynomial vanishes to order m at (a, b) if
the terms in the above expression for it satisfy k + l 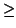 m whenever
the coefficients
m whenever
the coefficients
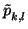 are non-zero.
are non-zero.
Exercise 24
If P and Q vanish to order m at a point,
then so does
R . P + Q for any polynomial R.
Because of this we can work with arithmetic operations on polynomials
``modulo'' terms that vanish to order m at a given point
(a, b). In particular, any polynomial is like a linear
polynomial upto terms that vanish to order two.
As before
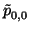 is the value of P at (a, b).
is the value of P at (a, b).
Exercise 25
If we denote the rule
P 
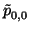
by
(
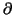
/
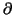 x
x)
|(a, b)
then check that this is a constant derivation.
We also have polynomial derivations and as before
Exercise 26
Any polynomial derivation is determined by what it does to the two
variables x and y.
In particular we have
(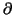 /
/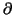 x) which is defined as the
derivation that sends x to 1 and y to 0;
x) which is defined as the
derivation that sends x to 1 and y to 0;
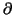 /
/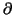 y is
defined by symmetry.
y is
defined by symmetry.
Exercise 27
Repeat this subsection replacing two variables x and
y with n variables
(x1,..., xn).



Next: Sequences
Up: Polynomials and polynomial functions
Previous: Polynomials in one variable
Kapil H. Paranjape
2001-01-20