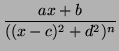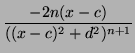Next: Polynomials in more than
Up: Polynomials and polynomial functions
Previous: Polynomials and polynomial functions
A polynomial P in one variable x is formally defined as a follows
P(x) = p0 + p1x + ... + pnxn
where the pi are constants. If n = 0 we identify the polynomial
with the constant p0. If pn 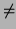 0 then we say the polynomial has
degree n. If pn = 0 then we drop the corresponding term unless
n = 0; the degree of the constant polynomial 0 is considered
undefined.
0 then we say the polynomial has
degree n. If pn = 0 then we drop the corresponding term unless
n = 0; the degree of the constant polynomial 0 is considered
undefined.
Exercise 9
Define the arithmetic operations on polynomials algorithmically so
that polynomial manipulations can be implemented on a computer.
Polynomials can be ``evaluated'' to give functions; for any choice of
a of constant b, we can substitute x by b to obtain the
``value'' of the polynomial; this gives us the function associated
with a polynomial. However, note that when the field of constants is
finite (e. g. the field with two elements
F2) a non-constant
polynomial might induce a constant function.
Exercise 10
Give an example of a polynomial that is not constant but gives a
constant function on the field with three elements.
The points where the function associated with the polynomial
vanishes are called solutions or roots of the polynomial.
Exercise 11
Let P(x) be a polynomial of degree n in one variable. The
constant b is a root of P (i. e. P(b) = 0) if and only if
P(x) can be written as a product (x - b)Q(x) where Q(x) has
degree n - 1. Hence or otherwise show that P(x) has at most n
roots.
The polynomial x2 + 1 has no roots over the field of real
numbers. The field of complex numbers is collection of numbers of the
form
a + b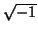 ; where a and b are real numbers.
; where a and b are real numbers.
Exercise 12
Define the arithmetic operations on complex numbers algorithmically
in terms of the arithmetic operations on real numbers. Show that any
quadratic polynomial x2 + ax + b is a product
(x - d )(x - c) over the
field of complex numbers (d and c need not be distinct).
The Fundamental Theorem of Algebra states that any polynomial
over the field of real numbers is a product of linear and quadratic
terms upto a non-zero constant multiple. Thus any polynomial with real
coefficients has all its roots over complex numbers.
Exercise 13
Assuming the fundamental theorem of algebra show that any polynomial
with complex coefficients has all its roots over complex numbers.
In the above discussion, we used the phrase ``has all its roots'' as a
synonym for writing the polynomial as a product of linear terms. Now
if some of these factors repeat then we say we have repeated or
multiple roots. In particular, we can say that (x - b)k vanishes k
times at b.
Exercise 14
Use the Binomial theorem to write a polynomial of
P degree
n as
follows
P(
x) =
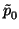
+
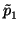
(
x -
b) +
... +
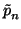
(
x -
b)
n
for some constants
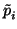
.
Thus we can say that a polynomial vanishes to order k at b if the
terms in the above expression for it satisfy
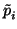 = 0 whenever
i < n.
= 0 whenever
i < n.
Exercise 15
If P and Q vanish to order k at b, then so does
R . P + Q for any polynomial R.
Note that
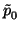 is the value P(b) of P at b. Moreover,
the term
is the value P(b) of P at b. Moreover,
the term
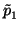 depends on P and on b that we will
now to determine. Suppose that we have
depends on P and on b that we will
now to determine. Suppose that we have
| P(x) |
= |
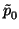 + + 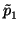 (x - b) + terms that vanish to order 2 at b (x - b) + terms that vanish to order 2 at b |
|
| Q(x) |
= |
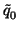 + + 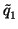 (x - b) + terms that vanish to order 2 at b (x - b) + terms that vanish to order 2 at b |
|
| R(x) |
= |
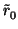 + + 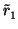 (x - b) + terms that vanish to order 2 at b (x - b) + terms that vanish to order 2 at b |
|
The above algebraic property of vanishing to order n shows us that
Thus, if we denote the rule that associates the constant
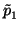 with
P as
(d /dx)| b, then this satisfies
with
P as
(d /dx)| b, then this satisfies
(d /dx)| b(R . P + Q) = (d /dx)| b(R)P(b) + R(b)(d /dx)| b(P) + (d /dx)| b(Q)
Such a rule (which takes polynomial to constants) is called a
(constant) derivation. If we formally replace b by the
variable x we obtain the requirement for a polynomial derivation
(which takes polynomial to polynomial). A polynomial derivation is a
rule D which associates to every polynomial P another polynomial
D(P) so that
D(R . P + Q) = R . D(P) + D(R) . P + D(Q).
and D(c) = 0 for a constant polynomial c.
Exercise 16
For any derivation D and any polynomial P show that
D(Pn) = nPn - 1D(P). (Hint: Use induction). Hence or otherwise show that a
derivation is determined on all polynomials once one knows what it
does to the variable x.
In particular, for there is a derivation which takes x to 1. This is
called the derivative with respect to x and is denoted by dP/dx.
Exercise 17
Show that the value of dP/dx at b is
(d /dx)| b(P).
The relation between derivations and the order of vanishing is given
by
Exercise 18
If P vanishes to order n at b then D(P) vanishes to order
n - 1 (for any derivation D).
One of the aims of calculus is to find a larger class of functions
which can be studied in a manner analogous to that given above for
polynomials. To do this we need to generalise the notion of
``vanishing to order n'' and derivations.
A simple way to enlarge the class is to consider ``rational
functions'', constructed from polynomials the same way as fractions are
from natural numbers. A rational function is of the form P/Q where
P and Q are polynomials with Q 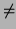 0.
0.
Exercise 19
Extend the definitions of the arithmetic operations and d /dx to
rational functions.
Let P and Q be any polynomials. The usual division algorithm
allows us to write an expression P = RQ + S , where R and S are
polynomials and the degree of S is less than that of Q or S is
zero. Using this and the fundamental theorem of algebra it is not
difficult to show
Exercise 20
Every rational function over real numbers is the sum of terms of the
form
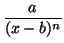
and/or
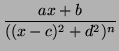
This the called the partial fraction expansion.
Given a polynomial P consider the problem of trying to find a
polynomial Q so that dQ/dx = P. This is quite easily solved using
the fact (proved above) that
d (xn)/dx = nxn - 1. When the problem
is posed for rational functions it becomes a bit harder.
Hence given any rational function P/Q over reals the only hurdle to
solving the problem of finding a function f so that df /dx = P/Q is
to solve this when P/Q is either 1/(x - b) or
(ax + b)/((x - c) + d2). In the section on integration we will see how these
problems can be solved.



Next: Polynomials in more than
Up: Polynomials and polynomial functions
Previous: Polynomials and polynomial functions
Kapil H. Paranjape
2001-01-20
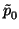 +
+ 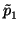 (x - b) + ... +
(x - b) + ... + 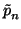 (x - b)n
(x - b)n
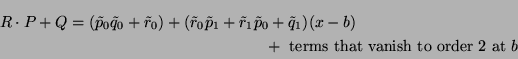
![]() 0.
0.