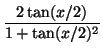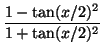Next: About this document ...
Up: Pre-requisites
Previous: Curves
We are now in a position to introduce many interesting
functions. In particular, we define and obtain properties of the
exponential and trigonometric functions.
Recall, that the rational functions that could not be integrated in
terms of rational functions were of the form 1/(x - b) or
(ax + b)/((x - c)+d2). The former is a continuous function when x 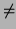 b
and the latter is continuous for all x. Thus we study the two
functions
b
and the latter is continuous for all x. Thus we study the two
functions
The function A(x) is called the logarithm denoted by log(x) and
the function B(x) is the inverse of the tangent function denoted by
tan-1(x) or
arctan(x).
Exercise 61
Show that the function A(x) is monotonic and goes to infinity as
x goes to infinity.
In particular, it follows that A has an inverse. This function is
called the exponential function and denoted by exp(x). We can
define the number e as exp(1); it is called Napier's natural base
for the logarithm.
Exercise 62
Show that e is between 2 and 4.
Now the fundamental property of the logarithm is
Exercise 63
Show that
A(x + y) = A(x) + A(y). Consequently we obtain
exp(xy) = exp(x)exp(y).
This property and the monotonicity of exp characterise it.
Exercise 64
Let f (x) be a monotonic function so that
f (xy) = f (x)f (y) and
f (x) = a. Show that
f (x) = exp(x log(a)).
Finally, we can define the hyperbolic functions as usual,
cosh(x) = 1/2(exp(x) + exp(- x)) and so on.
We noe study the functions related with the function B.
Exercise 65
Show that the function B(x) is monotonic and remains bounded as
x goes to infinity.
The least upper bound of the numbers 2B(x) is denoted by 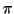 . We
can thus define the function tan(x) on the range
(-
. We
can thus define the function tan(x) on the range
(- 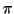 /2,
/2,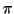 /2) as the inverse of B.
/2) as the inverse of B.
Exercise 66
Show that an arclength parametrisation of the unit circle
x2 +
y2 = 1 is given by
t 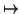
(sin(
t), cos(
t)) where
we define these functions by the formulae
| sin(x) |
= |
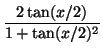 |
|
| cos(x) |
= |
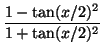 |
|
Note that it follows that the perimeter of the circle
x2 +
y2 = 1 is
2
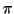
.
It is thus natural to extend these functions periodically for
all t. We can define a multiplication on the unit circle by
(x1, y1)·(x2, y2) = (x1x2 - y1y2, x1y2 + x2y1)
Exercise 67
Show that the arclength parametrisation gives a group homomorphism
from the additive group of real numbers to the circle.
This exercise provides the link between the trigonometric and
exponential function which is expressed by the formula
exp(
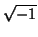 x
x) = cos(
x) +
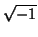
sin(
x)



Next: About this document ...
Up: Pre-requisites
Previous: Curves
Kapil H. Paranjape
2001-01-20
![]() b
and the latter is continuous for all x. Thus we study the two
functions
b
and the latter is continuous for all x. Thus we study the two
functions