


Next: Elementary functions
Up: Pre-requisites
Previous: Integration
Now that we have a basic understanding of differentiability of
functions we can begin the study of plane curves which can be defined
parametrically or as the locus of vanishing of a function of two
variables. At the very least we need the function to be (piecewise)
differentiable with ``good'' first order properties. We shall see
later that for any interesting (and æsthetic!) study
we will need second derivatives as well.
A plane curve is defined (locally) as the locus of points where a
``good'' function f of two variables vanishes. In particular, let
p = (a, b) be a point where f vanishes, then we assume that
f (x, y) = f1, 0(x - a) + f0, 1(y - b) + o(x) is continuously differentiable at this point. The curve is said to be
singular at p if both the above coefficients are 0; otherwise
we call the curve non-singular or smooth. For a smooth
curve through p the line
f1, 0(x - a) + f0, 1(y - b) = 0 is called
the tangent line. It is the ``best'' linear approximation to the curve
in an obvious way:
Exercise 57
Consider the natural parametrisation of the line

(
x -
a) +

(
y -
b) = 0. The restriction of the function
f to
this line can then be thought of as a function of one variable.
Show that this function vanishes to order 2 if and only if the line
is the one above
or the curve
f = 0 is singular at the point
p = (
a,
b).
In what follows we restrict our attention to smooth curves. Singular
curves are very interesting and are studied extensively in algebraic
geometry.
A different way of representing curves is to think of a curve as a
``moving point''. A curve can be given in parametric form by writing a
pair of functions
(x(t), y(t)) so that as t varies we will trace
out a curve. As before we will insist on the two functions being
continuously differentiable. We say that our curve is non-singular
at ``time'' t = t0 we need at least of the pair
(x'(t0), y'(t0)) to be
non-zero; otherwise we call the curve singular.
Exercise 58
Consider the function of
t given by substituting the above pair of
functions in the linear form
l (
x,
y) =
 x
x +
 y
y +

.
Show that this function vanishes to order 2 at
t =
t0 if and only
if the curve is singular
or the form
l (
x,
y) is the
tangent form
y'(
t0)(
x -
x(
t0)) -
x'(
t0)(
y -
y(
t0)).
We need to have some way of going from the parametric form of a curve
to the equation and vice verse. For the first problem, let us assume
(without loss of generality) that
x'(t0) 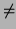 0. Then, by the
inverse function theorem, we have g(x) so that g(x(t)) = t, so that
we can re-parametrise the curve to get
(x, y(g(x)). The curve is the
(locally) given by the equation y - h(x) = 0 where
h(x) = y(g(x).
0. Then, by the
inverse function theorem, we have g(x) so that g(x(t)) = t, so that
we can re-parametrise the curve to get
(x, y(g(x)). The curve is the
(locally) given by the equation y - h(x) = 0 where
h(x) = y(g(x).
To go from the equation to the parametric form we need to show that
lines parallel to a line which is not tangent to the curve will
meet the curve in exactly one point near the given point. This done
through the implicit function theorem. (Note to author: Exercises to
be added here).
One of the advantanges of working with ``orders'' of vanishing is that
make these theorems ``explicit'' if we only need our equations to be
satisfied upto terms of some order. For example, we say that
(x(t), y(t)) is a parametrisation at t = t0 upto order r of the
curve
f (x(t), y(t)) = o((t - t0)r). Similarly, two curves, f and g
are said to osculate upto order r if
f - g = o(xr). In
particular, any curve osculates upto order 2 with a conic; thus it is
possible to write a parametrisation upto order two quite explicitly.
Finally, there is one distinguished parametrisatisation. Let
(x(t), y(t)) be a curve. Thinking of this as a moving point we have
not only a tangent line but a tangent vector (called the velocity
vector)
(x'(t), y'(t)). It is thus natural to define the speed
of the curve as length of this vector.
We can ask for a constant speed (or more accurately constant energy)
parametrisation. In other words, can we find t = u(s) so that
(x'(t)2 + y'(t)2) | t = u(s)u'(s)2 = constant
Exercise 59
Use the inverse function theorem to show that the function
s(
t) =

has an inverse. Show that this inverse
function satisfies the above equation.
We will see that such a parametrisation called parametrisation by
arc-length plays an important role in geometry. Meanwhile,
Exercise 60
Show that to obtain such a parametrisation for the circle, we need
to solve the equation
u'(
t)
2
= 1
(Hint: Use the following parametrisation.)
We will study the solution of this and related equations in the next
section.



Next: Elementary functions
Up: Pre-requisites
Previous: Integration
Kapil H. Paranjape
2001-01-20