


Next: 11.2 Shanks' Baby step-Giant
Up: 11 Algorithms for groups
Previous: 11 Algorithms for groups
This method uses the least amount of information about the group and
also uses the least amount of storage. We choose a ``random''
partition of the elements of the group into disjoint sets S0,
S1, ..., Sr (which are specified by their membership functions
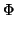 ). We now define a collection of maps as follows. Start with a
``random'' element x0 of the group. Let
v0 = (0,..., 0) be the
origin in the group
). We now define a collection of maps as follows. Start with a
``random'' element x0 of the group. Let
v0 = (0,..., 0) be the
origin in the group
 r. We define an iterated map as follows
r. We define an iterated map as follows
(
xi + 1,
vi + 1) =
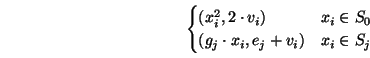
(
xi,
vi) =
 giai
giai = 1
Some aspects of Brent's method can be used to further ensure that
vi does not grow too large (since we are only interested in
v2T - vT). Assuming that the choice of Si is ``random''
enough we should be close to a relation of the smallest size in the
sense that
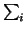 ai is the shortest. That is also an estimate of
the number of steps upto a small constant factor.
ai is the shortest. That is also an estimate of
the number of steps upto a small constant factor.



Next: 11.2 Shanks' Baby step-Giant
Up: 11 Algorithms for groups
Previous: 11 Algorithms for groups
Kapil Hari Paranjape
2002-10-20
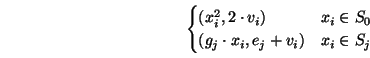 (xi, vi) =
(xi, vi) =