


Next: 11.1 Pollard's
Up: Some Lectures on Number
Previous: 10.3 Cryptanalytic methods
The following section is loosely based on the study of algorithms for
groups as in the work of Schoup, Schnorr, Buchmann and others. How
does one specify a group to a computer? First of all the elements of
the group are represented by ``words'' of some fixed length
(bitstrings of a fixed length). Let us denote the set of such words by
F. However, since the group does not have order a power of two, not
all such words will be elements of the group. Thus we have a
membership function
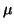 : F
: F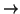 {0, 1} that takes the value 1 for
elements of the group. We then have the group operations which
usually ``expand'' the word length. In other words we have a superset
F2 containing F which has ``double words'' (words of twice the
size of those in F) and the group multiplication operation usually
gives
m : F×F
{0, 1} that takes the value 1 for
elements of the group. We then have the group operations which
usually ``expand'' the word length. In other words we have a superset
F2 containing F which has ``double words'' (words of twice the
size of those in F) and the group multiplication operation usually
gives
m : F×F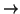 F2. There is usually also an inverse
operation
i : F2
F2. There is usually also an inverse
operation
i : F2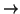 F2 which takes F to itself; more often a
``ratio'' operation
d : F×F
F2 which takes F to itself; more often a
``ratio'' operation
d : F×F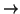 F2 is provided instead. Finally,
there is a reduction operation
r : F2
F2 is provided instead. Finally,
there is a reduction operation
r : F2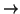 F. The actual group
operations are defined by
F. The actual group
operations are defined by
| x . y |
= |
r(m(x, y)) |
|
| x . y-1 |
= |
r(d (x, y)) |
|
| x-1 |
= |
r(i(x, y)) |
|
This specification should satisfy the condition that these operations,
when restricted to the set
G = 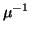 (1) satisfy the axioms for an
abelian group. We will assume that such a collection of operations has
indeed been provided to us as a ``black box''. We will look at
algorithms that study the properties of this group without
looking into the details of how the maps
(1) satisfy the axioms for an
abelian group. We will assume that such a collection of operations has
indeed been provided to us as a ``black box''. We will look at
algorithms that study the properties of this group without
looking into the details of how the maps 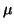 , m, d and r are
defined. Some have called this the study of ``generic group
algorithms''.
, m, d and r are
defined. Some have called this the study of ``generic group
algorithms''.
One way to represent a finite abelian group G and compute its
structure is to write it via generators and relations. Suppose we are
given a collection g1, g2, ..., gr of generators of G and
we can find a collection 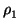 ,
, 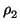 , ...,
, ..., 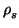 of
relations of the form
of
relations of the form
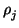
=
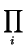 giaij
giaij
If this collection of relations is sufficient, we obtain an exact
sequence
where A is given by the matrix (aij) and g the ``vector'' of
generators of G. Such a description reduces the computation of the
abstract structure of G to matrix manipulations. For example,
by reducing the matrix to echelon form we can exhibit an isomorphism
from a product of cyclic groups to the group G. However,
it is not so easy(!) to write the inverse of this isomorphism. To do that
one must exhibit a (computable) set-theoretic splitting
G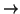
 r.
One way to compute such a splitting on an element g of G is to
find enough relations between g and the collection of the gi's.
It is thus clear that the important problem in the algorithmic
analysis of finite abelian groups is that of finding (sufficiently
many) relations between elements of the group.
r.
One way to compute such a splitting on an element g of G is to
find enough relations between g and the collection of the gi's.
It is thus clear that the important problem in the algorithmic
analysis of finite abelian groups is that of finding (sufficiently
many) relations between elements of the group.
There are essentially three classes of ``generic group algorithms''
which can be called the Pollard 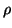 method, Shanks' Baby Step Giant
Step method and the Pohlig-Hellman factor method. We illustrate these
methods by seeing how they can be used to find a relation between some
given elements g1, g2, ..., gr of the group.
method, Shanks' Baby Step Giant
Step method and the Pohlig-Hellman factor method. We illustrate these
methods by seeing how they can be used to find a relation between some
given elements g1, g2, ..., gr of the group.
Subsections



Next: 11.1 Pollard's
Up: Some Lectures on Number
Previous: 10.3 Cryptanalytic methods
Kapil Hari Paranjape
2002-10-20
![]() ,
, ![]() , ...,
, ..., ![]() of
relations of the form
of
relations of the form
![]() method, Shanks' Baby Step Giant
Step method and the Pohlig-Hellman factor method. We illustrate these
methods by seeing how they can be used to find a relation between some
given elements g1, g2, ..., gr of the group.
method, Shanks' Baby Step Giant
Step method and the Pohlig-Hellman factor method. We illustrate these
methods by seeing how they can be used to find a relation between some
given elements g1, g2, ..., gr of the group.