


Next: 1.4 Using the shift
Up: 1 Multiple Precision Arithmetic
Previous: 1.2 Multiplication Algorithm
This is by far the most complicated procedure. The first point to note
is that the school method for long division involves a ``guess''. We
need to ensure that this guess is replaced a multiple-choice procedure
(also characterised by a ``case'' statement). Moreover, the number of
choices should be very small and not of the same size as the base M.
As for the case of multiplication we can understand some aspects of
the relevant book-keeping by performing the ``short'' division
(v1 ... vq) = u×(w1 ... wq) + t
where t < u. We first compute
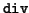 (u, 0, v1) = (w1, t1). From then on
we have the inductive approach
(u, 0, v1) = (w1, t1). From then on
we have the inductive approach
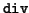 (u, ti, vi + 1) = (wi + 1, ti + 1). Clearly, the first step is a
special case of the second by putting v0 = 0. At the end t = tq.
Moreover, there are exactly q steps.
(u, ti, vi + 1) = (wi + 1, ti + 1). Clearly, the first step is a
special case of the second by putting v0 = 0. At the end t = tq.
Moreover, there are exactly q steps.
There are two procedures for long division, each with its own level of
complexity. We note that in the division
(v0 ... vq) = (u1 ... uq)×w + (t1 ... tq)
where v0 < u1 and
(t1 ... tq) < (u1 ... uq), a ``good guess'' for w
is provided by x which is obtained by
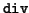 (u1, v0, v1) = (x, y)
(so that y < u1). The following lemma tells us just
how good the guess is
(u1, v0, v1) = (x, y)
(so that y < u1). The following lemma tells us just
how good the guess is
Lemma 1
If
2
. u1 + 1
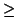 M
M then we have
x - 2
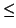 w
w 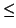 x
x.
Proof.
Using
(
u2 ... uq)
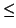 Mq - 1
Mq - 1 - 1 and
(
v2 ... vq)
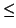 Mq - 1
Mq - 1 we obtain the
following inequalities
| u1 . Mq - 1 |
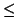 (u1 ... uq) (u1 ... uq) 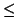 |
u1Mq - 1 + Mq - 1 - 1 |
|
| (v0 . M + v1) . Mq - 1 |
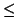 (v0 ... vq) (v0 ... vq) 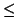 |
(v0 . M + v1) . Mq - 1 + Mq - 1 - 1 |
|
which we can combine with the Euclidean inequalities
| u1 . x |
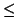 v0 . M + v1 v0 . M + v1 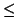 |
u1 . (x + 1) - 1 |
|
| (u1 ... uq)×w |
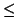 (v0 ... vq) (v0 ... vq) 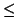 |
(u1 ... uq)×(w + 1) - 1 |
|
We then obtain
As a consequence
w < (
x + 1) or equivalently (since these are
integers)
w 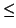 x
x. The reverse comparison is provided by
It follows that
u1 . x < (
u1 + 1)
. (
w + 1) or (since we have
integers on both sides)
u1 . x 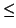 u1 .
u1 . (
w + 1) +
w. Now the
condition
v0 <
u1 implies that
x 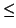
(
M - 1). So if
w 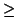 M
M - 1,
then we certainly have the inequality
x 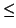 w
w + 2 as required. Thus
we may assume that
w <
M - 1. From the assumption
2
. u1 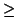 M
M - 1
we obtain
w <
u1 . 2. Combining this with the above we see
that
u1 . x 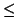 u1 .
u1 . (
w + 1) +
w <
u1 . (
w + 3)
or equivalently
x 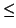 w
w + 2 as required.
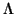
Using this lemma, we see that we can give an algorithm for the long
division
(v1 ... vp) = (u1 ... uq)×(w0 ... wr) + (t1 ... ts)
that involves making one out of three choices. In order to apply the
lemma we must first normalise the divisor
(u1 ... uq). So as a
first step we compute
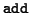 (u1, 1, 0) = (t,
(u1, 1, 0) = (t,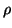 ). If
). If 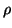 = 1, then we
take d = 1, other wise we compute
= 1, then we
take d = 1, other wise we compute
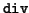 (t, 1, 0) = (d, r). Thus in every
case we have d is the integer part of M/(u1 + 1). We now take
(t, 1, 0) = (d, r). Thus in every
case we have d is the integer part of M/(u1 + 1). We now take
| (x1 ... xq) |
= |
d×(u1 ... uq) |
|
| (y0 ... yp) |
= |
d×(v1 ... vp) |
|
Here we take y0 = 0 if necessary. We check easily that this step
also ensures that y0 < x1. Next we initialise
(t0, 0 ... t0, q - 1) = (y0 ... yq - 1).
We can then perform the long division
by induction as follows. Let
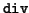 (x1, ti, 0, ti, 1) = (gi, r); then gi
is our guess. We compute (and note that the z sequence cannot be
longer than q due to the choice of gi)
(x1, ti, 0, ti, 1) = (gi, r); then gi
is our guess. We compute (and note that the z sequence cannot be
longer than q due to the choice of gi)
(
ti, 0 ... ti, q - 1yq + i) -
gi×(
x1 ... xq) = (
zi, 0 ... zi, q - 1) -
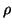 . Mq
. Mq
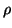 = 0 then we take
(ti + 1, 0 ... ti + 1, q - 1) = (zi, 0 ... zi, q - 1) and wi = gi.
Otherwise (we have
= 0 then we take
(ti + 1, 0 ... ti + 1, q - 1) = (zi, 0 ... zi, q - 1) and wi = gi.
Otherwise (we have 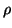 = 1 and) we compute
= 1 and) we compute
(
zi, 0 ... zi, q - 1) + (
x1 ... xq) = (
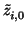 ...
... 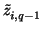
) +
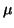 . Mq
. Mq
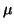 = 1 then we take
(ti + 1, 0 ... ti + 1, q - 1) = (
= 1 then we take
(ti + 1, 0 ... ti + 1, q - 1) = (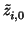 ...
... 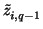 ) and
) and
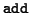 (gi, 1, 0) = (wi, 0). Finally, if we have
(gi, 1, 0) = (wi, 0). Finally, if we have 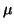 = 0, then we put
= 0, then we put
(
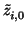 ...
... 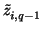
) + (
x1 ... xq) = (
ti + 1, 0 ... ti + 1, q - 1) +
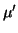 . Mq
. Mq
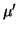 = 1 is ensured by the lemma above. We put
= 1 is ensured by the lemma above. We put
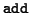 (gi, 2, 0) = (wi, 0) in this case. After r = p - q steps we obtain the
identity
(gi, 2, 0) = (wi, 0) in this case. After r = p - q steps we obtain the
identity
(y0 ... yp) = (x1 ... xq)×(w0 ... wr) + (tr + 1, 0 ... tr + 1, q - 1)
From the choices for x's and y's we see that d exactly divides
the remainder, so we perform short division to obtain
(tr + 1, 0 ... tr + 1, q - 1) = d×(t1 ... tq)
This completes the long division which takes about 3rq steps
upto terms linear in p and q (such as additions and subtractions).
Another way to simplify the guessing process is to take
(u0u1 ... uq)
of the form
(10u2 ... uq). In this case, the division of
(v0 ... vq) always yields one of v0 or v0 - 1 as the
quotient. The main question is then how to perform the necessary
normalisation (to bring the u into this form). Starting with
(u1 ... uq) we first compute
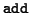 (u1, 1, 0) = (t,
(u1, 1, 0) = (t,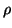 ) and if
) and if
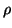 = 1 we put d = 1. Otherwise, we compute
= 1 we put d = 1. Otherwise, we compute
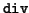 (t, 1, 1) = (d, r).
Thus, in every case d is the integer part of
(M + 1)/(u1 + 1). As
before, we multiply by d
(t, 1, 1) = (d, r).
Thus, in every case d is the integer part of
(M + 1)/(u1 + 1). As
before, we multiply by d
| (x1, 0 ... x1, q) |
= |
d×(u1 ... uq) |
|
| (y1, 0 ... y1, p) |
= |
d×(v1 ... vp) |
|
Where we put x1, 0 = 0 and y1, 0 = 0 if there is no carry over.
Now, if xi, 1 = 0 (then xi, 0 = 1 is forced) we stop. Otherwise,
we perform the following steps
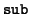 (0, x1, 1, 0) (0, x1, 1, 0) |
= (ci, 1) |
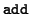 (x1, 1), 1, 0) (x1, 1), 1, 0) |
= (ti,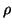 ) ) |
|
if 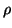 = 0 = 0 |
|
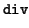 (ti, ci, 0) (ti, ci, 0) |
= (di, r) |
|
if 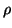 = 1 = 1 |
|
di |
= ci |
|
Thus in every case, we have di is the integer part of
M(M - x1, 1)/(xi, i + 1). Now, we multiply by (1.di)
| (xi + 1, 0 ... xi + 1, q.xi + 1, q + 1 ... ) |
= |
(1.di)×(xi, 0 ... xi, q.xi, q + 1 ... ) |
|
| (yi + 1, 0 ... yi + 1, p.yi + 1, q + 1 ... ) |
= |
(1.di)×(yi, 0 ... yi, q.yi, q + 1 ... ) |
|
where we use the (.) to keep the notation simple and note that there
are only finitely many terms after it. We now iterate over i.
Lemma 2
For some
i 
3 we obtain
(
xi, 0xi, 1xi, 2 ... ) = (10
xi, 2 ... ) as required.
Assuming this for the moment we see that have removed all  operations in the iterative part of the long division process. We
leave it to the reader to make an algorithm out of this procedure.
The proof of the lemma is a somewhat complicated exercise which we
skip as well.
operations in the iterative part of the long division process. We
leave it to the reader to make an algorithm out of this procedure.
The proof of the lemma is a somewhat complicated exercise which we
skip as well.



Next: 1.4 Using the shift
Up: 1 Multiple Precision Arithmetic
Previous: 1.2 Multiplication Algorithm
Kapil Hari Paranjape
2002-10-20
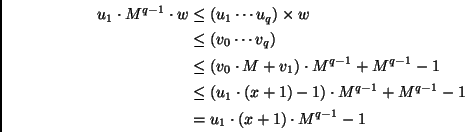
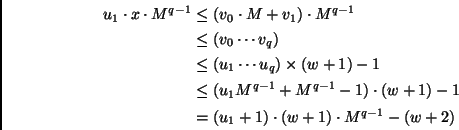
![]() (u1, 1, 0) = (t,
(u1, 1, 0) = (t,![]() ) and if
) and if
![]() = 1 we put d = 1. Otherwise, we compute
= 1 we put d = 1. Otherwise, we compute
![]() (t, 1, 1) = (d, r).
Thus, in every case d is the integer part of
(M + 1)/(u1 + 1). As
before, we multiply by d
(t, 1, 1) = (d, r).
Thus, in every case d is the integer part of
(M + 1)/(u1 + 1). As
before, we multiply by d