


Next: 1.3 Long Division Algorithm
Up: 1 Multiple Precision Arithmetic
Previous: 1.1 Addition and Subtraction
As is to be expected, multiplication is more complicated. The usual
method of multiplication requires simultaneous summation of multiple
rows of decimal numbers. The carry over from addition thus becomes
quite large, whereas our basic routines can only handle a carry of 0
or 1. It is best to proceed slowly!
First of all we look at a procedure to multiply by a single ``digit''
u and perform the calculation,
u×(v1 ... vp) = (w0w1 ... wp).
Actually we will need the more general ``linear form'' operation
(we will assume that q 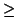 p + 1 by padding t by zeros if necessary)
p + 1 by padding t by zeros if necessary)
u×(v1 ... vp) + (t0 ... tq) = (w0 ... wq + 1)
More diagrammatically,
| |
|
|
v1 |
v2 |
... |
vp - 1 |
vp |
| × |
|
|
|
|
|
|
u |
| + |
t0 |
t1 |
t2 |
t3 |
... |
tq - 1 |
tq |
| |
|
x1 |
x2 |
x3 |
... |
xp |
|
| |
|
|
y1 |
y2 |
... |
yp - 1 |
yp |
| z0 |
z1 |
z2 |
z3 |
... |
zq - 1 |
zq |
zq + 1 |
| w0 |
w1 |
w1 |
w2 |
... |
wq - 1 |
wq |
wq + 1 |
The usual multiplication procedures leads to certain intermediate
digits which we denote by x, y, z as above. We obtain
the identities
| (xp, yp) |
= |
 (u, vp) (u, vp) |
|
(wq + 1, ) ) |
= |
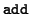 (tp, y0, 0) (tp, y0, 0) |
|
(zq, ) ) |
= |
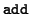 (tq - 1, xp, 0) (tq - 1, xp, 0) |
|
| (xp - i, yp - i) |
= |
 (u, vp - i) (u, vp - i) |
|
(wq + 1 - i, ) ) |
= |
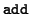 (zq + 1 - i, yp - i, (zq + 1 - i, yp - i, ) ) |
|
(zq - i, ) ) |
= |
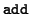 (tq - i - 1, xp - i, (tq - i - 1, xp - i, ) ) |
|
As before the first three steps are a special case of the latter three
when we put
 = 0 =
= 0 =  and zp = tp. There are q + 2 cycles.
The
and zp = tp. There are q + 2 cycles.
The
 operation actually takes place only in the first p cycles
(in the remaining cases xj and yj are zero). The last
operation actually takes place only in the first p cycles
(in the remaining cases xj and yj are zero). The last
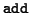 operation does not take place on the last cycle. Thus, are at most
p + 2q + 3 steps.
operation does not take place on the last cycle. Thus, are at most
p + 2q + 3 steps.
Now we use the above routine repeatedly to obtain the general linear
form, (where as before we assume that
s 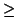 p + q + 1)
p + q + 1)
(u1 ... up)×(v1 ... vq) + (t0 ... ts - 1) = (w0 ... ws)
We see that this is achieved by intermediate computations of the form
| up×(v1 ... vq) + (t0 ... ts - 1) |
= |
(z0, p ... zs, p) |
|
| up - i×(v1 ... vq) + (z0, p - i + 1 ... zs - i, p - i + 1) |
= |
(z0, p - i ... zs - i, p - i) |
|
Then
ws - i = zs - i, p - i since the (s - i)-th ``digit''
zs - i, p - i is not affected by subsequent computations. If we
initialise
(z0, p + 1 ... zs, p + 1) to be equal to
(t0, ... ts - 1), then first computation is a special case of the second. We
will perform p cycles, each a linear form as above of the length
q + 2s + 3. Thus the number of steps is order of pq + 2ps + 3p steps.
While this looks a bit complex, it is still not the most efficient
when the p and q are large enough to allow us to use more (order
linear in p and q) ``book-keeping'' steps in exchange for
efficiency.



Next: 1.3 Long Division Algorithm
Up: 1 Multiple Precision Arithmetic
Previous: 1.1 Addition and Subtraction
Kapil Hari Paranjape
2002-10-20
![]() p + 1 by padding t by zeros if necessary)
p + 1 by padding t by zeros if necessary)
![]() p + q + 1)
p + q + 1)