


Next: 7 Quadratic fields
Up: 6 Algebraic Number Fields
Previous: 6.6 Minkowski's Geometry of
Another way to write generators of groups of ideals is to use prime
ideals. An ideal P of R is prime if for every a and b in R
so that ab lies in P at least one of a and b lies in P; an
equivalent assertion is that R/P is a domain--non-zero elements
give non-zero products. It is clear that the restriction
P 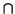
 satisfies the same conditions for integers a and b. In other words
P
satisfies the same conditions for integers a and b. In other words
P 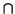
 is generated by a prime number p. Thus P determined by
the ideal P/pR in R/pR. Now, if
R =
is generated by a prime number p. Thus P determined by
the ideal P/pR in R/pR. Now, if
R =  . w1 + ... +
. w1 + ... +  . wn, then R/pR is a vector space of rank n over the finite field
. wn, then R/pR is a vector space of rank n over the finite field
 /p
/p . Instead of solving this specific problem, we can ask for
a structure theorem for commutative rings with identity with
underlying additive group a vector space of rank n over
. Instead of solving this specific problem, we can ask for
a structure theorem for commutative rings with identity with
underlying additive group a vector space of rank n over
 /p
/p .
.
Lemma 15
Any ring with underlying additive group a finite dimensional vector
space over

/
p
is a direct sum of rings of the form
(

/
p
)[
T]/(
P(
T)
m), where
P(
T) is an irreducible
polynomial over the field

/
p
.
This result follows from the Chinese Remainder theorem and Euclidean
division applied to the polynomial ring in one variable
( /p
/p )[T]. If we use the symbol
)[T]. If we use the symbol
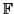 q to denote the field
with q elements (where q is a prime power), then this result can
be refined further as follows
q to denote the field
with q elements (where q is a prime power), then this result can
be refined further as follows
Lemma 16
The ring
(

/
p
)[
T]/(
P(
T)
m), where
P(
T) is an irreducible
polynomial of degree
d, is isomorphic to the ring
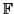 pd
pd[
h]/(
hn).
This result follows by constructing (using Newton's method of
successive approximations) a polynomial 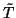 of the form
T + P(T)Q1(T) + ... + P(T)n - 1Qn - 1(T) so that
P(
of the form
T + P(T)Q1(T) + ... + P(T)n - 1Qn - 1(T) so that
P(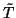 ) is
divisible by P(T)n. Then
h =
) is
divisible by P(T)n. Then
h = 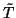 - T. Combining these results,
we see that R/pR has the form
Corresponding to each factor we get a surjective ring homomorphism
R/pR
- T. Combining these results,
we see that R/pR has the form
Corresponding to each factor we get a surjective ring homomorphism
R/pR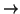
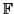 pfi. The kernel of this has the form Pi/pR for
a prime ideal Pi whose restriction is p. The number fi is
called the residual degree (or more simply the degree) of Pi over
p, while the number ei is called the ramification degree (or order
of ramification) of Pi over p.
pfi. The kernel of this has the form Pi/pR for
a prime ideal Pi whose restriction is p. The number fi is
called the residual degree (or more simply the degree) of Pi over
p, while the number ei is called the ramification degree (or order
of ramification) of Pi over p.
Now, let I be any ideal. Suppose first that the restriction i of
I is of the form i1i2, with i1 and i2 co-prime. We can
apply the Chinese Remainder theorem to write R/I as a direct sum of
R/I1 and R/I2, where
I1 = I + i1R and
I2 = I + i2R. Thus
I = I1 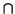 I2; if I is invertible one easily shows that
I = I1 . I2. Thus we can reduce our study of groups of ideals to
the study of ideals Q so that the restriction q is the power of a
prime p. Now, R/(Q + pR) is a quotient of the ring studied above and
is not zero. Thus there is a prime Pi as above so that Q is
contained in Pi. By successively removing such Pi (if Q is
invertible) we can write Q as a product of various powers of the
Pi considered above. Thus we have written any invertible ideal as a
product of (invertible) prime ideals. It is not difficult to show that
any such product expression is unique. Thus, we obtain the unique
factorisation of ideals in terms of prime ideals.
I2; if I is invertible one easily shows that
I = I1 . I2. Thus we can reduce our study of groups of ideals to
the study of ideals Q so that the restriction q is the power of a
prime p. Now, R/(Q + pR) is a quotient of the ring studied above and
is not zero. Thus there is a prime Pi as above so that Q is
contained in Pi. By successively removing such Pi (if Q is
invertible) we can write Q as a product of various powers of the
Pi considered above. Thus we have written any invertible ideal as a
product of (invertible) prime ideals. It is not difficult to show that
any such product expression is unique. Thus, we obtain the unique
factorisation of ideals in terms of prime ideals.



Next: 7 Quadratic fields
Up: 6 Algebraic Number Fields
Previous: 6.6 Minkowski's Geometry of
Kapil Hari Paranjape
2002-10-20
![% latex2html id marker 16521
$\displaystyle {\frac{{\mathbb F}_{p^{f_1}}[h_1]}{(h_1^{e_1})}}$](img162.png)
![% latex2html id marker 16524
$\displaystyle {\frac{{\mathbb F}_{p^{f_g}}[h_g]}{(h_g^{e_g})}}$](img164.png)
![]() I2; if I is invertible one easily shows that
I = I1 . I2. Thus we can reduce our study of groups of ideals to
the study of ideals Q so that the restriction q is the power of a
prime p. Now, R/(Q + pR) is a quotient of the ring studied above and
is not zero. Thus there is a prime Pi as above so that Q is
contained in Pi. By successively removing such Pi (if Q is
invertible) we can write Q as a product of various powers of the
Pi considered above. Thus we have written any invertible ideal as a
product of (invertible) prime ideals. It is not difficult to show that
any such product expression is unique. Thus, we obtain the unique
factorisation of ideals in terms of prime ideals.
I2; if I is invertible one easily shows that
I = I1 . I2. Thus we can reduce our study of groups of ideals to
the study of ideals Q so that the restriction q is the power of a
prime p. Now, R/(Q + pR) is a quotient of the ring studied above and
is not zero. Thus there is a prime Pi as above so that Q is
contained in Pi. By successively removing such Pi (if Q is
invertible) we can write Q as a product of various powers of the
Pi considered above. Thus we have written any invertible ideal as a
product of (invertible) prime ideals. It is not difficult to show that
any such product expression is unique. Thus, we obtain the unique
factorisation of ideals in terms of prime ideals.