


Next: 6.7 Prime ideals
Up: 6 Algebraic Number Fields
Previous: 6.5 Groups of invertible
In order to decide whether or not a lattice M is of the form
 . R (and hence trivial in the class group) we need to find
elements
. R (and hence trivial in the class group) we need to find
elements  in M whose norm is as close as possible to that of
M. This is achieved in the following section.
in M whose norm is as close as possible to that of
M. This is achieved in the following section.
We now want to give a ``measure'' associated with an order R. The
space of n×n matrices with rational entries is naturally
contained in the space of n×n matrices with real entries. Thus
we can consider the ring
 . K of real linear combinations of
elements of K. This is an n-dimensional vector space over
. K of real linear combinations of
elements of K. This is an n-dimensional vector space over
 .
Thus, for any lattice M, the space
TM =
.
Thus, for any lattice M, the space
TM =  . K/M is an
n-dimensional torus. Taking some translation invariant measure on
. K/M is an
n-dimensional torus. Taking some translation invariant measure on
 . K gives us a notion of volume for the tori TM with the
property that
vol(TM) = vol(TR)Nm(M). Now, if A is any (compact
measurable) subset of
. K gives us a notion of volume for the tori TM with the
property that
vol(TM) = vol(TR)Nm(M). Now, if A is any (compact
measurable) subset of
 . K with the property that
vol(A) > vol(TM) then the map A
. K with the property that
vol(A) > vol(TM) then the map A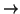 TM cannot be one-to-one (with
a little thought it is clear that this is actually also true if
vol(A)
TM cannot be one-to-one (with
a little thought it is clear that this is actually also true if
vol(A) 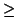 vol(TM)). The difference between two points with the
same inverse image will give a non-zero element of M.
vol(TM)). The difference between two points with the
same inverse image will give a non-zero element of M.
Now, one natural way to identify
 . K with
. K with
 n (and thus
put a measure on it) is to use ``simultaneous diagonalisation''. As
seen above K is generated by a single n×n matrix
n (and thus
put a measure on it) is to use ``simultaneous diagonalisation''. As
seen above K is generated by a single n×n matrix  whose characteristic polynomial P(T) is irreducible over rationals.
This means that this has distinct roots and so over real numbers can
be brought into a ``diagonal'' form as below by a suitable change of
co-ordinates.
whose characteristic polynomial P(T) is irreducible over rationals.
This means that this has distinct roots and so over real numbers can
be brought into a ``diagonal'' form as below by a suitable change of
co-ordinates.
Here
 denote the real roots of P(T), while
(
denote the real roots of P(T), while
( ,
, ) are the pairs
of conjugate complex roots of P(T). Now, every element of K is a
linear combination of powers of
) are the pairs
of conjugate complex roots of P(T). Now, every element of K is a
linear combination of powers of  so that it too is brought
into the above form by the same change of co-ordinates. For
simplicity of notation we write the matrix associated with an element
so that it too is brought
into the above form by the same change of co-ordinates. For
simplicity of notation we write the matrix associated with an element
 of K as
[
of K as
[ ,...,
,..., ,
, ,...,
,..., ].
More generally, for any element x in
].
More generally, for any element x in
 . K we have a
representation
[x(1),..., x(r1),
. K we have a
representation
[x(1),..., x(r1), ,...,
,..., ].
This representation gives us an identification of
].
This representation gives us an identification of
 . K with
. K with
 n. If
R =
n. If
R =  . w1 + ... +
. w1 + ... +  wn, then the volume of
TR, with respect to this identification is the determinant of the
n×n matrix
wn, then the volume of
TR, with respect to this identification is the determinant of the
n×n matrix  given by
given by

=
 wi(1)
wi(1),...,
wi(r1), Re

, Im

,..., Re

, Im


Let the matrix
 (complex entries) be given by
(complex entries) be given by

=
 wi(1)
wi(1),...,
wi(r1),

,

,...,

,


Standard rules for column operations on determinants show that the
determinant of
 is 2r2 times the determinant of
is 2r2 times the determinant of
 . On the other hand the (i, j)-th entry of the matrix
. On the other hand the (i, j)-th entry of the matrix
 .
.  is
which we immediately recognise as
Trace(wi . wj) when it
is expressed in the form given above. Combining these observations
we obtain the identity
vol(TR) = (1/2r2)
is
which we immediately recognise as
Trace(wi . wj) when it
is expressed in the form given above. Combining these observations
we obtain the identity
vol(TR) = (1/2r2) .
.
Now consider the region A consisting of all x in
 . K so
that
| x(i)|
. K so
that
| x(i)| 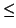 ai and
|
ai and
| |
| 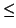 bi for some
positive constants ai and bj. We have
bi for some
positive constants ai and bj. We have
Thus, in order to obtain a pair (v1, v2) in A so that v = v1 - v2
is a non-zero element of M we need the condition
Now the norm of the element v is the product
Nm(
v) =

|
v1(i) -
v2(i)|
. 
|

-

|
2 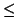
2
r1 ai
ai×2
2r2 bj2
bj2
Lemma 14
For any ideal
I of an order
R in
K there is a non-zero element
v in
I so that
Here we have written |
R/
I| instead of
Nm(
I) in order to make
the dependence on
R clear.
Proof.
We just combine the inequality above with the condition that needs
to be satisfied in order to obtain such a
v.
In particular, if I is an invertible ideal, then
vR = I . J where
J = vR . I-1 and
Nm(J) 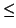 (2/
(2/ )r2
)r2 . Now,
for any element of the class group
Cl(R), let I represent the
inverse of this class. The above argument produces a representative
J of the class which has norm no more than
(2/
. Now,
for any element of the class group
Cl(R), let I represent the
inverse of this class. The above argument produces a representative
J of the class which has norm no more than
(2/ )r2
)r2 . In particular, we have shown than the
class group is finite (an ideal J of norm n is a quotient of
cardinality n the group R/nR; there are at most finitely many such
quotient groups).
. In particular, we have shown than the
class group is finite (an ideal J of norm n is a quotient of
cardinality n the group R/nR; there are at most finitely many such
quotient groups).
While it is not too difficult to use this procedure to write all the
ideals J satisfying the above condition, it is much harder to write
the ``multiplication table'' for the group
Cl(R) on the basis of
what has gone so far. If J1 and J2 are two ideals as above and
the product no longer satisfies the above condition, then we need to
find the element v in
(J1 . J2) that the lemma
guarantees. But the proof of the lemma gives us no way to find such
elements!



Next: 6.7 Prime ideals
Up: 6 Algebraic Number Fields
Previous: 6.5 Groups of invertible
Kapil Hari Paranjape
2002-10-20
![]() . K of real linear combinations of
elements of K. This is an n-dimensional vector space over
. K of real linear combinations of
elements of K. This is an n-dimensional vector space over
![]() .
Thus, for any lattice M, the space
TM =
.
Thus, for any lattice M, the space
TM = ![]() . K/M is an
n-dimensional torus. Taking some translation invariant measure on
. K/M is an
n-dimensional torus. Taking some translation invariant measure on
![]() . K gives us a notion of volume for the tori TM with the
property that
vol(TM) = vol(TR)Nm(M). Now, if A is any (compact
measurable) subset of
. K gives us a notion of volume for the tori TM with the
property that
vol(TM) = vol(TR)Nm(M). Now, if A is any (compact
measurable) subset of
![]() . K with the property that
vol(A) > vol(TM) then the map A
. K with the property that
vol(A) > vol(TM) then the map A![]() TM cannot be one-to-one (with
a little thought it is clear that this is actually also true if
vol(A)
TM cannot be one-to-one (with
a little thought it is clear that this is actually also true if
vol(A) ![]() vol(TM)). The difference between two points with the
same inverse image will give a non-zero element of M.
vol(TM)). The difference between two points with the
same inverse image will give a non-zero element of M.
![]() . K with
. K with
![]() n (and thus
put a measure on it) is to use ``simultaneous diagonalisation''. As
seen above K is generated by a single n×n matrix
n (and thus
put a measure on it) is to use ``simultaneous diagonalisation''. As
seen above K is generated by a single n×n matrix ![]() whose characteristic polynomial P(T) is irreducible over rationals.
This means that this has distinct roots and so over real numbers can
be brought into a ``diagonal'' form as below by a suitable change of
co-ordinates.
whose characteristic polynomial P(T) is irreducible over rationals.
This means that this has distinct roots and so over real numbers can
be brought into a ``diagonal'' form as below by a suitable change of
co-ordinates.

![]() . K so
that
| x(i)|
. K so
that
| x(i)| ![]() ai and
|
ai and
|![]() |
| ![]() bi for some
positive constants ai and bj. We have
bi for some
positive constants ai and bj. We have