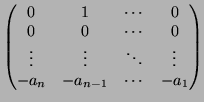Next: 6.3 Orders and Maximal
Up: 6 Algebraic Number Fields
Previous: 6.1 Algebraic Numbers
Let n be any positive integer and consider a sub-algebra K of the
algebra of n×n matrices with rational entries; by this we mean
that K contains scalar multiples of the identity matrix and is
closed under matrix addition, subtraction and multiplication. To
handle division we also insist that non-zero matrices in K are
invertible (this actually implies that the inverses are also in K
but it is not entirely trivial to prove this). Finally, one knows that
the algebra of matrices is not commutative for n 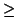 2. So we put in
an additional hypothesis that matrix multiplication between elements
of K is commutative.
2. So we put in
an additional hypothesis that matrix multiplication between elements
of K is commutative.
Now, consider the map

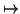
 . v where v is any
(fixed) non-zero column vector such as the transpose of
(1, 0..., 0). When
. v where v is any
(fixed) non-zero column vector such as the transpose of
(1, 0..., 0). When  and
and 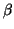 are an elements of K with
are an elements of K with
 . v =
. v = 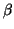 . v, we obtain
(
. v, we obtain
( -
- 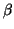 ) . v = 0. But
we have assumed that every non-zero element of K is invertible so we
must have
) . v = 0. But
we have assumed that every non-zero element of K is invertible so we
must have
 -
- 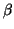 = 0. In other words this map is one-to-one on K. Thus K is actually isomorphic to a vector
space of rank at most n over the rationals. By a suitable change of
basis (and restricting to a submatrix) we may as well assume that the
space K . v contains all column vectors or equivalently
that K has rank n. Then K . w is the space of all column
vectors for any non-zero vector w. We will henceforth make
this additional assumption as well.
= 0. In other words this map is one-to-one on K. Thus K is actually isomorphic to a vector
space of rank at most n over the rationals. By a suitable change of
basis (and restricting to a submatrix) we may as well assume that the
space K . v contains all column vectors or equivalently
that K has rank n. Then K . w is the space of all column
vectors for any non-zero vector w. We will henceforth make
this additional assumption as well.
For any n×n matrix  we have (the Cayley-Hamilton
theorem) that characteristic polynomial
ch
we have (the Cayley-Hamilton
theorem) that characteristic polynomial
ch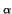 (T) of
degree n and
ch
(T) of
degree n and
ch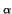 (
( ) = 0. (In the words of one
mathematician khudh kaa nahi satisfy karega to kiska satisfy
karega?(Hindi); if it doesn't satisfy its' own then whose will it
satisfy?). On the other hand, we have the minimal
polynomial
) = 0. (In the words of one
mathematician khudh kaa nahi satisfy karega to kiska satisfy
karega?(Hindi); if it doesn't satisfy its' own then whose will it
satisfy?). On the other hand, we have the minimal
polynomial
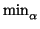 (T), which is the polynomial of least degree
with rational coefficients that is satisfied by
(T), which is the polynomial of least degree
with rational coefficients that is satisfied by  . If
. If
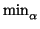 (T) = P(T)Q(T), then
P(
(T) = P(T)Q(T), then
P( )Q(
)Q( ) = 0. Since,
P(
) = 0. Since,
P( ) and Q(
) and Q( ) are in K at least one of them must be
zero thus one of them must be a constant; in other words the minimal
polynomial is irreducible. It also follows as before that it
divides the characteristic polynomial. One can show that, under the
hypothesis of the previous paragraph (and the fact the we are working
over rationals; a perfect field), there is an element
) are in K at least one of them must be
zero thus one of them must be a constant; in other words the minimal
polynomial is irreducible. It also follows as before that it
divides the characteristic polynomial. One can show that, under the
hypothesis of the previous paragraph (and the fact the we are working
over rationals; a perfect field), there is an element  in K whose characteristic polynomial is irreducible, i. e.
its characteristic polynomial equals its minimal polynomial. In
particular, the field K has a basis over the field
in K whose characteristic polynomial is irreducible, i. e.
its characteristic polynomial equals its minimal polynomial. In
particular, the field K has a basis over the field
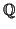 of
rationals of the form 1,
of
rationals of the form 1,  , ...,
, ...,
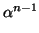 .
.
Proof.
[(Sketch of Proof)] Let
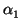
,
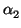
, ...,
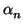
be a basis of
K over the field
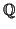
. Consider the
characteristic polynomial of
T1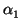
+ ... +
Tn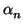
as
a function of the
variables T1, ...,
Tn. The condition
that this is reducible will impose certain non-trivial polynomial
relations between the
Tk's. Thus all we need to do is to find
rational numbers
rk that do not satisfy these relations. Then the
characteristic polynomial of

=
r1
+ ... +
rn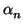
will be irreducible (and of degree
n. It follows
that, the elements 1,

, ...,
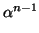
will be
independent over
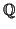
.
To summarise, we will henceforth think of an algebraic number field as
a sub-algebra of the ring of n×n matrices which is commutative,
with all non-zero elements being invertible. Moreover, this algebra
contains an element  whose characteristic polynomial P(T)
is equal to its minimal polynomial. An further extension of the above
argument then shows that any invertible matrix g that commutes
with every element of K is contained in K; we will use this in
later sections.
whose characteristic polynomial P(T)
is equal to its minimal polynomial. An further extension of the above
argument then shows that any invertible matrix g that commutes
with every element of K is contained in K; we will use this in
later sections.
As an example, let us consider the ``construction'' of the field
associated with an irreducible polynomial
P(T) = Tn + a1Tn - 1 + ... + an. We consider the matrix
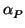
=
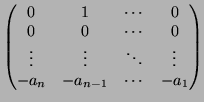
This has minimal polynomial and characteristic polynomial equal to
P(T). The sub-algebra of matrices generated by 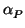 is the
required field
is the
required field
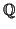 (
(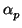 ), sometimes also denoted by
), sometimes also denoted by
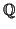 [T]/(P(T)) (one uses Euclid's algorithm for polynomials to show
that every non-zero element of this is invertible). The above
discussion says that any field under consideration is isomorphic
to a field of this form for some irreducible polynomial P(T).
[T]/(P(T)) (one uses Euclid's algorithm for polynomials to show
that every non-zero element of this is invertible). The above
discussion says that any field under consideration is isomorphic
to a field of this form for some irreducible polynomial P(T).



Next: 6.3 Orders and Maximal
Up: 6 Algebraic Number Fields
Previous: 6.1 Algebraic Numbers
Kapil Hari Paranjape
2002-10-20
![]()
![]()
![]() . v where v is any
(fixed) non-zero column vector such as the transpose of
(1, 0..., 0). When
. v where v is any
(fixed) non-zero column vector such as the transpose of
(1, 0..., 0). When ![]() and
and ![]() are an elements of K with
are an elements of K with
![]() . v =
. v = ![]() . v, we obtain
(
. v, we obtain
(![]() -
- ![]() ) . v = 0. But
we have assumed that every non-zero element of K is invertible so we
must have
) . v = 0. But
we have assumed that every non-zero element of K is invertible so we
must have
![]() -
- ![]() = 0. In other words this map is one-to-one on K. Thus K is actually isomorphic to a vector
space of rank at most n over the rationals. By a suitable change of
basis (and restricting to a submatrix) we may as well assume that the
space K . v contains all column vectors or equivalently
that K has rank n. Then K . w is the space of all column
vectors for any non-zero vector w. We will henceforth make
this additional assumption as well.
= 0. In other words this map is one-to-one on K. Thus K is actually isomorphic to a vector
space of rank at most n over the rationals. By a suitable change of
basis (and restricting to a submatrix) we may as well assume that the
space K . v contains all column vectors or equivalently
that K has rank n. Then K . w is the space of all column
vectors for any non-zero vector w. We will henceforth make
this additional assumption as well.
![]() we have (the Cayley-Hamilton
theorem) that characteristic polynomial
ch
we have (the Cayley-Hamilton
theorem) that characteristic polynomial
ch![]() (T) of
degree n and
ch
(T) of
degree n and
ch![]() (
(![]() ) = 0. (In the words of one
mathematician khudh kaa nahi satisfy karega to kiska satisfy
karega?(Hindi); if it doesn't satisfy its' own then whose will it
satisfy?). On the other hand, we have the minimal
polynomial
) = 0. (In the words of one
mathematician khudh kaa nahi satisfy karega to kiska satisfy
karega?(Hindi); if it doesn't satisfy its' own then whose will it
satisfy?). On the other hand, we have the minimal
polynomial
![]() (T), which is the polynomial of least degree
with rational coefficients that is satisfied by
(T), which is the polynomial of least degree
with rational coefficients that is satisfied by ![]() . If
. If
![]() (T) = P(T)Q(T), then
P(
(T) = P(T)Q(T), then
P(![]() )Q(
)Q(![]() ) = 0. Since,
P(
) = 0. Since,
P(![]() ) and Q(
) and Q(![]() ) are in K at least one of them must be
zero thus one of them must be a constant; in other words the minimal
polynomial is irreducible. It also follows as before that it
divides the characteristic polynomial. One can show that, under the
hypothesis of the previous paragraph (and the fact the we are working
over rationals; a perfect field), there is an element
) are in K at least one of them must be
zero thus one of them must be a constant; in other words the minimal
polynomial is irreducible. It also follows as before that it
divides the characteristic polynomial. One can show that, under the
hypothesis of the previous paragraph (and the fact the we are working
over rationals; a perfect field), there is an element ![]() in K whose characteristic polynomial is irreducible, i. e.
its characteristic polynomial equals its minimal polynomial. In
particular, the field K has a basis over the field
in K whose characteristic polynomial is irreducible, i. e.
its characteristic polynomial equals its minimal polynomial. In
particular, the field K has a basis over the field
![]() of
rationals of the form 1,
of
rationals of the form 1, ![]() , ...,
, ...,
![]() .
.