Thus, one way to specify an algebraic number ![]() is as follows.
First we give P(t) which is the non-zero polynomial (with rational
or integer coefficients) of least degree such that
P(
is as follows.
First we give P(t) which is the non-zero polynomial (with rational
or integer coefficients) of least degree such that
P(![]() ) = 0 (by
Euclidean division applied to polynomials it follows that P divides
any other Q for which
Q(
) = 0 (by
Euclidean division applied to polynomials it follows that P divides
any other Q for which
Q(![]() ) = 0). Further, we need to specify a
number x0 of the form
r + s .
) = 0). Further, we need to specify a
number x0 of the form
r + s . ![]() with r and s rational
so that successive iterations of Newton's method
with r and s rational
so that successive iterations of Newton's method
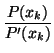
Another way is to make use of Hensel's lemma. We will define below the
discriminant DP for a polynomial P. For now it suffices that if a
prime p does not divide DP then for any n so that p divides
P(n), we have that p does not divide P'(n). In other words DP
is the least common multiple of
gcd(P(n), P'(n)) as n varies over
all integers. Now, for n sufficiently large it is clear that there
is such a prime p (i. e. not dividing DP) so that p divides
P(n). We can now specify ![]() by saying that is should be congruent to n modulo p. Because of Hensel's lemma (which is
Newton's iteration done modulo powers of p!) we can then produce
nk so that
by saying that is should be congruent to n modulo p. Because of Hensel's lemma (which is
Newton's iteration done modulo powers of p!) we can then produce
nk so that
![]() - nk is divisible by pk for every k. In
modern language, we are replacing the approximation by complex numbers
given above by a p-adic approximation. We can actually, find a
suitable p so that this can be done for all roots of the
polynomial P. (This is a particular case of Chebychev's density
theorem).
- nk is divisible by pk for every k. In
modern language, we are replacing the approximation by complex numbers
given above by a p-adic approximation. We can actually, find a
suitable p so that this can be done for all roots of the
polynomial P. (This is a particular case of Chebychev's density
theorem).
An entirely less obvious problem is how we can perform common arithmetic operations on algebraic numbers when they are represented in this fashion. For that reason, and for the reason mentioned at the beginning of this section we now turn to the matrix representation of algebraic numbers.