Lemma 10 (Hensel's lemma)
Let
f (
T) =
Td +
a1Td - 1 + ... +
ad be a (monic) polynomial with
integer coefficients
ai. Let
n be an integer so that
f (
n) is
divisible by
p, and
f'(
n) =
dnd - 1 +
a1(
d - 1)
nd - 2 + ... +
ad - 1
is not divisible by
p. Then there is a sequence of integers
nk
for every
k 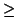
1, so that
n1 =
n,
nk + 1 -
nk is divisible by
pk and
f (
nk) is divisible by
pk. Moreover,
nk is
uniquely determined modulo
pk.
Proof.
The proof closely mimics Newton's method of finding roots. Having
already found
nk we need to find
nk + 1 =
nk +
bkpk so that
f (
nk + 1) is divisible by
pk + 1. By the binomial expansion
(or Taylor series!),
f (nk + bkpk) = f (nk) + bkpkf'(nk)(mod pk + 1)
using
2
k 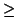 k
k + 1 since
k 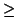
1. We are given
f (
nk) =
ckpk for
some constant
ck. Moreover,
nk =
n(mod
p) so
f'(
nk) =
f'(
n)(mod
p) is an invertible element of

/
p
. Let
m be an inverse so that
mf'(
nk) = 1(mod
p). We
put
bk = -
mck and obtain the required condition.