


Next: 4.5 Hensel's lemma
Up: 4 Primes and Composites
Previous: 4.3 Combinations of the
We now look at tests that will try to show that a number is
composite. In other words, the test either shows that the number is
composite or exits (apparently) without giving any information.
If p is a prime number, then all numbers between 1 and p - 1 give
units in
 /p
/p . In fact,
. In fact,
 /p
/p is a field and we
have the elementary result
is a field and we
have the elementary result
Lemma 6
The group of units in a finite field is a cyclic group.
Proof.
By Legendre's theorem we see that the order of any element divides
the order of the group. On the other hand, if
x has order dividing
d then it is a solution of
Td - 1; the latter has at most
d
solutions since we are in a field. Thus, the exponent of the group
of units (i. e. the least common multiple of the orders) must be
equal to the order of the group. Now, given elements
x and
y of
orders
m and
n in an abelian group it is easy to construct an
element of the form
xayb which has order equal to the least
common multiple of
m and
n. Thus we have a unit of order equal
to the order of the group of units; in words the group is cyclic.
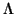
In particular, by Legendre's theorem we see that ap - 1 = 1 in
 /p
/p for any non-zero element a. Thus if we wish to check
whether a number N is composite we can try to find a so that
aN - 1
for any non-zero element a. Thus if we wish to check
whether a number N is composite we can try to find a so that
aN - 1 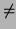 1 in
1 in
 /N
/N . This is already a good check to see
that N does not have square factors.
. This is already a good check to see
that N does not have square factors.
Lemma 7
When
N is an odd number that has square factors, let us define the
set of ``bad'' elements
S
Then, the cardinality of
S is at most 2
N/9. If
N has no prime
factors smaller than
p this can be improved to
(
p - 1)
N/
p2.
The proof depends on the following very important result
Proposition 8
The group of units in

/
pe
is cyclic for any
odd
prime number
p and any
e 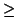
1.
We will defer the proof of this proposition to the next subsection.
Proof.
(of the lemma)
Since
N is odd and has square factors there is an odd prime
p
and an
e 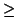
2 so that
pe is the exact power that divides
N.
Any element
a 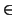 S
S gives an element
b in

/
pe
so that
bN - 1 = 1. Since the latter group is cyclic of order
pe -
pe - 1 it follows that the number of possible values of
b
is
gcd(
N - 1,
pe -
pe - 1) (exercise!). Since
p divides
N, this
GCD is equal to
gcd(
N - 1,
p - 1), which is not more than
p - 1. The
fraction of such
b's is thus at most (
p - 1)/
p2 (since
e 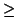
2). By the Chinese remainder theorem, the set
S is the same
fraction of elements of

/
N
.
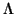
While this result is useful to know, one can write numbers (which are
called Carmichael numbers) such as
N = 561 = 3×11×17, with the
property that the order of every unit in
 /N
/N divides
N - 1. The necessary improvement on the test was suggested by Miller
and Rabin.
divides
N - 1. The necessary improvement on the test was suggested by Miller
and Rabin.
We write N = 1 + q2k with q odd. Now, when N is a prime,
 /N
/N is a field. Thus, the only element other than 1 whose
square is 1 is -1. It follows that for any a
is a field. Thus, the only element other than 1 whose
square is 1 is -1. It follows that for any a 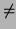 0, either
aq = 1 or there is some e between 0 and k - 1 so that
aq2e = - 1. Now we have seen that computing powers in
0, either
aq = 1 or there is some e between 0 and k - 1 so that
aq2e = - 1. Now we have seen that computing powers in
 /N
/N is easily done. Thus we can pick any a and form the powers
aq2e for
0
is easily done. Thus we can pick any a and form the powers
aq2e for
0 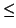 e < k in succession. If aq
e < k in succession. If aq 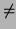 1 and none of
these powers is -1, then N must be composite. On the other hand,
it could happen that for all the a's we pick either aq = 1 or some
aq2e = - 1. In this case we appear to have obtained no information.
However, we have
1 and none of
these powers is -1, then N must be composite. On the other hand,
it could happen that for all the a's we pick either aq = 1 or some
aq2e = - 1. In this case we appear to have obtained no information.
However, we have
Lemma 9
Let
N be a composite number of the form 1 +
q2
k. Let us define
the set of ``bad'' elements
T = {
a 
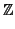
/
N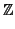
|
aq = 1 or
aq2e = - 1 for some
e with
0
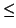 e
e <
k }
Then, the cardinality of
T is less than
N/4.
Proof.
Let us write the prime factorisation
N =
p1e1 ... prer.
Now, if
a is in
T, then clearly
aq2k = 1, so
a is also in
the set
S defined earlier. Since 2
N/9 <
N/4 (!) we may as well
assume that
ei = 1 for all
i. In other words, we assume that
N
is a product of distinct prime factors. Now, we write
pi = 1 +
qi2
ki with
qi odd; for later use we note that
k is
not less than the minimum of the
ki's. We further decompose
T
into the set
T-1 = {
a|
aq = 1} and the sets (for 0
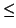 e
e <
k)
Te = {a| aq2e = - 1}
Then, elements of
T-1 reduce to units in

/
pi
which
have order dividing
q. This is a subgroup of order
gcd(
q,
pi - 1) = gcd(
q,
qi). Thus, by the Chinese remainder theorem
#T-1 = gcd(q, q1) ... gcd(q, qr)
The elements of
Te, can be characterised as elements, whose
q-th power has order
exactly 2
e + 1. These
q-th powers
then have order exactly 2
e + 1 when reduced modulo
pi. In
particular, this means that
e <
ki for every
i; the other
Te's
are empty. There are exactly
gcd(
q,
qi)2
e + 1 elements in

/
pi
with order dividing
q2
e + 1 and among these a
subgroup of index 2 has elements of order dividing
q2
e (a
subgroup of a cyclic group is cyclic). Thus, by Chinese remainder
theorem we obtain
#Te = gcd(q, q1) ... gcd(q, qr) . 2re
Thus we see that the cardinality of
T is
gcd(
q,
q1)
... gcd(
q,
qr)

1 +

2
re
= gcd(
q,
q1)
... gcd(
q,
qr)



where
l is the minimum of the
ki's. Now, the Chinese remainder
theorem shows that the number of units in

/
N
is precisely
q1 ... qr . 2
 ki
ki; this is at least one less than
N. Thus the proportion of elements in
T is strictly smaller than
 .
. 
The first term is no more than 1, while the second is no more than
1/2
r - 1 (note that
l 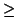
1). Thus, we obtain the result unless
r = 2. Moreover, if
k2 >
k1 (or vice versa) then we see that the
second term is no more than 1/2
r so we have the result in this
case as well. Thus we may assume that
k1 =
k2 =
l. Now, if
gcd(
q,
q1) <
q1 then (since these are odd numbers and one divides
the other)
gcd(
q,
q1)
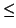
3
q1. This implies that the above
expression is no more than 1/6. Thus, we may further assume that
gcd(
q,
q1) =
q1. By expanding the identity
(1 +
q2
k) = (1 +
q12
l)(1 +
q22
l) we see that
gcd(
q,
q1) = gcd(
q,
q2). Since the
primes
p1 and
p2 are distinct
q1 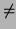 q2
q2; thus
q1 = gcd(
q,
q1)
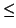
3
q1 as above. Now we again obtain that the
above expression is no more than 1/6. This completes the argument.
What the above reasoning amounts to is that if we choose uniformly among all possible a's in
 /N
/N , there is a
chance of less than 1/4 that we will pick an a which gives ``no
information'' as the output of our test even though N is composite.
This is not ``no information'' at all! If we repeat this test n
times there is a chance of less than (1/4)n that N is composite
and we did not detect it. It seems more than reasonable to call an N
that satisfies such a test a strong pseudo-prime. When we
specify the a1, a2, ..., an, we say that N is a strong
pseudo-prime with bases a1, a2, ..., an.
, there is a
chance of less than 1/4 that we will pick an a which gives ``no
information'' as the output of our test even though N is composite.
This is not ``no information'' at all! If we repeat this test n
times there is a chance of less than (1/4)n that N is composite
and we did not detect it. It seems more than reasonable to call an N
that satisfies such a test a strong pseudo-prime. When we
specify the a1, a2, ..., an, we say that N is a strong
pseudo-prime with bases a1, a2, ..., an.
While have not actually proved that N is a prime in such a case
(unlike trial division) there appears to be good enough reason to
treat it like a prime. In later sections we will look at primality
tests and primality certificates. It is clear that we should not even
attempt those unless we have already put our N through the
Miller-Rabin grinder and it has come out successful!



Next: 4.5 Hensel's lemma
Up: 4 Primes and Composites
Previous: 4.3 Combinations of the
Kapil Hari Paranjape
2002-10-20
![]() /p
/p![]() . In fact,
. In fact,
![]() /p
/p![]() is a field and we
have the elementary result
is a field and we
have the elementary result
![]() /N
/N![]() is a field. Thus, the only element other than 1 whose
square is 1 is -1. It follows that for any a
is a field. Thus, the only element other than 1 whose
square is 1 is -1. It follows that for any a ![]() 0, either
aq = 1 or there is some e between 0 and k - 1 so that
aq2e = - 1. Now we have seen that computing powers in
0, either
aq = 1 or there is some e between 0 and k - 1 so that
aq2e = - 1. Now we have seen that computing powers in
![]() /N
/N![]() is easily done. Thus we can pick any a and form the powers
aq2e for
0
is easily done. Thus we can pick any a and form the powers
aq2e for
0 ![]() e < k in succession. If aq
e < k in succession. If aq ![]() 1 and none of
these powers is -1, then N must be composite. On the other hand,
it could happen that for all the a's we pick either aq = 1 or some
aq2e = - 1. In this case we appear to have obtained no information.
However, we have
1 and none of
these powers is -1, then N must be composite. On the other hand,
it could happen that for all the a's we pick either aq = 1 or some
aq2e = - 1. In this case we appear to have obtained no information.
However, we have

 .
. 