The Ultimate in Anty-Particles

by Ian Stewart

The hotel lobby was in a state of pandemonium, with suitcases and backpacks piled all over the place. I wondered for the hundredth time whether I'd been in my right mind even to consider attending the Quinquennial SPAM World Convention. I took one look at the check-in line and headed for the hotel bar. About half the participants at this meeting of the Society for Philosophizing about Mathematics had had the same idea.

Immediately to my left, a smartly dressed woman in her mid-sixties was engaged in a heated discussion with what appeared to be the epitome of teenage grunge. A thin woman with spiky hair wore a T-shirt labeled "Watch This Space." There was an overexcited fuzzicist who was busily explaining a flexible extension of conventional logic to three skeptical constructivists who wanted to make it more rigid. And a nerdish type in one corner was madly tapping the keys of a laptop computer.

I grinned and began to relax. The trip was going to be as intellectually rewarding as I had hoped, after all. I introduced myself to spiky hair and T-shirt, whose name turned out to be Louise. "I'm watching," I said.

"Uh?"

"'This Space.' I'm not seeing anything unexpected."

She gave me a funny look, as if she was trying to work out whether I was being sexist. "It's for the Equation," she said. "When they find it."

"The Equation?"

"Mind you, I'm not very hopeful of a quick breakthrough now that those idiots in Congress have canceled the Superconducting Super Collider."

"Oh, that equation," I said. "The Theory of Everything." She was a fundamentalist; I should have picked that up.

"You may scoff," she said. I started to shake my head to indicate that scoffing had not been on my mind. "I merely believe that everything in the universe is governed by one fundamental law and that the central aim of science must be to find out what it is."

"Yes, but even if it exists, what makes you think it's a mathematical law?" teenage grunge queried.

"The very word 'law' indicates a precision that can be found only in mathematics. Indeed, we can define mathematics as the study of the logical consequences of simple, precise laws."

"What do you mean exactly by 'logical'?" queried one of the constructivists.

"What do you mean by 'precise'?" asked the fuzzicist, who was called Inez. The convention was under way.

"The point is," Louise said, "once we find the laws of nature, we can deduce everything else. Instead of a messy patchwork of approximate theories, we'll know the truth."

"I think you're all on the wrong level of discussion," I interjected. "It's only 100 years or so since mathematicians proved that IN PRINCIPLE the entire future of the universe is determined by its present state and that led to a picture of a clockwork universe and the idea that simple laws necessarily generate simple behavior. But when people started to think seriously about what's possible in practice, they discovered chaos -- simple laws can generate extremely complex behavior, and deterministic systems can behave randomly. For the sake of argument, suppose you're right. Suppose that at base the universe really does obey a simple set of fundamental laws, and we find them. Will that really help us understand the world in which we live?"

"Of course it will," Louise answered. "First, it will provide a basic philosophical underpinning. Second, the behavior of our human-sized world is necessarily implicit in the fundamental laws, so the laws will explain everything."

"In principle, maybe. But not in practice. For instance, in the human-scale universe, cats like to chase mice. I wouldn't agree that your 'fundamental' laws explained that unless you could show me a convincing deduction, starting from your equations and ending with the fact that cats like to chase mice. How do you plan to do that?

"Even if you could carry the computations out, they would be impossibly huge and totally incomprehensible. No, the problem with Theories of Everything is that they start with the wrong concept of 'explanation.' An explanation is an explicit argument that leads from hypothesis to conclusion, not just a vague statement that the conclusion is implicit in the assumptions. And certainly not a stack of computer printouts 1,000 miles high that purports to render the implicit explicit."

The nerd in the corner woke up. "Let me show you all something." He plunked his laptop on the table. "Look at the screen." A fine grid of squares appeared. "That's an ant, okay?"

"Where?"

"Fascinating," Louise said. "Now, as I was saying about the Equation--"

"Louise," the nerd said, "if you'll let me explain what you just saw, you'll see that it is highly relevant to the topic under discussion."

"You always say that, Nathan, even when it's a game of Dougal the Dugong."

"Suspend judgment for a few minutes, and I'll justify my claim. What I've just shown you is a mathematical system known as Langton's ant. It's an amazingly simple cellular automaton invented by Chris Langton of the Santa Fe Institute."

"The complexity mob?"

"Precisely. They look for large-scale regularities in complex systems. Langton's ant is a simple example. The ant starts out on the central square, heading in some selected direction--say, east. It moves one square in that direction and looks at the color of the square it lands on--black or white. If it lands on a black square, it paints it white and turns 90 degrees to the left. If it lands on a white square, it paints it black and turns 90 degrees to the right. It keeps on following those same simple rules forever. You saw what happened when I started it on an all-white grid ."

"Surprisingly complex behavior for such a simple set of rules," I observed.

"You see, Louise, Langton's rules are the Theory of Everything for the universe that his ant inhabits. An anty-matter universe," he ended apologetically.

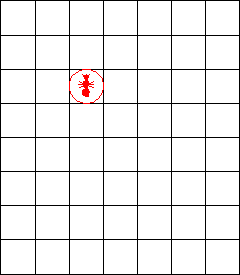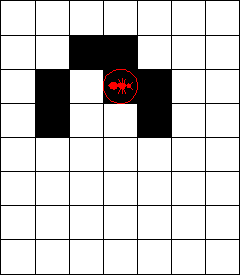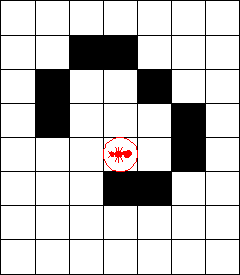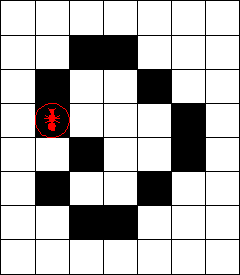
"Look at the strange sequence of shapes that the ant creates. For the first 500 or so steps, it keeps returning to the central square, leaving behind it a series of rather symmetrical patterns. Then, for the next 10,000 steps or so, the picture becomes very chaotic. Suddenly--almost as if the ant has finally made up its mind what to do--it builds what James Propp of the Massachusetts Institute of Technology, who first made the discovery, calls a highway. It repeatedly follows a sequence of precisely 104 steps that moves it two cells northwest and continues this indefinitely, forming a diagonal band ."

"The really amazing thing," Nathan went on, "is that it always seems to end up building a highway, even if you scatter black squares around the grid before it starts."

"I think," one of the constructivists said, "I can start it off next to an infinite line of black squares, and it will just follow them off to infinity. If I get the spacing just right."

"Sorry. Any FINITE arrangement of black squares. But nobody has ever been able to prove that the ant always builds a highway."

"Can anything general be proved about what Langton's ant does when it starts with any finite arrangement of black squares?"

"Yes," Nathan replied. "E.G.D. Cohen and X. P. Kong of the Rockefeller University proved that the ant's trajectory is necessarily unbounded. It escapes from any finite region [see "Cohen-Kong Theorem" below]."

"But what does it have to do with the Equation?" Louise asked.

"We know the Theory of Everything for Langton's ant," Nathan offered. "The rules. We set them up. But despite that, nobody can answer one simple question: Starting from an arbitrary 'environment' of finitely many black cells, does the ant always build a highway?"

"So here the Theory of Everything lacks explanatory power?" I wondered.

"Precisely. It predicts everything but explains nothing. In contrast, the Cohen-Kong theorem EXPLAINS why trajectories are unbounded."

"I can see several flaws in your argument," Louise noted. "First, the Cohen-Kong theorem is a CONSEQUENCE of the Theory of Everything, which therefore has at least some explanatory power. Next, your argument is founded on ignorance. Maybe tomorrow somebody will come up with a proof that ants always build highways."

"I agree. But it is making the Cohen-Kong consequence EXPLICIT that explains the unbounded trajectories. You can appeal to the uniqueness of the consequences of the Theory of Everything until you're blue in the face, but that alone won't tell you whether a bounded trajectory exists. Similarly, even though we know the Theory of Everything, we will have no idea whether highway building is the universal pattern until somebody makes it an explicit consequence. Or disproves it."

"Seems to me," I interrupted, "that you're asserting an awful lot based on just one exceptional example."

"Not really," Nathan countered. "Langton's ant is entirely typical of rule-based systems. There are lots of generalizations, and they exhibit surprising behaviors and, more surprising, common patterns. You can have fun putting one or more ants into a chosen environment and seeing what they do. You can change the rules and set up different environments--a hexagonal lattice, for instance, instead of a square grid. It's best done on a computer, where simple programs can implement the rules. I should add that there's also a practical side to these ideas: they relate to questions in statistical mechanics about arrays of particles--'ants'--that at any given moment can exist in only one of several states--'colored squares.'"

"Particles and anty-particles?"

"Thank you, Inez. Now, recently Greg Turk of Stanford University and, independently, Leonid A. Bunimovich of the Georgia Institute of Technology and S. E. Troubetzkoy of the University of Bielefeld investigated generalized ants defined by a rule-string. Suppose that instead of just black and white, the squares have n colors, labeled 0, 1, 2...n-1. The rule-string is a sequence of n symbols 0 or 1. When the ant leaves a cell of color k, it changes it to color k+1 (wrapping n=(n-1)+1 around to 0). It turns right if the kth symbol is 1 and left if it is 0. It moves one square on and repeats.

"Langton's original rules are summed up in rule-string 10. Some rule-strings give trivial ant dynamics--for example, an ant with rule-string 1 (or even 111...1) travels forever around a 2x2 square. But any rule-string that contains both 0 and 1 must lead to unbounded trajectories, by the Cohen-Kong idea.

"Suppose for simplicity you start with a 'clean' grid--all cells in color 0. Ant 100 creates patterns that start out looking rather like those of Langton's ant--at first symmetrical, then chaotic. After 150 million steps, however, it is still behaving chaotically. Does it ever build a highway? Nobody knows. Ant 110 does build a highway, and it takes only 150 steps to do so. Moreover, it needs a cycle of just 18 steps to create the highway, instead of the 104 used by Langton's ant. Ant 1000 is relentlessly chaotic. Ant 1101 begins chaotically but goes into highway construction after 250,000 steps, using a cycle of length 388. Ant 1100 keeps building ever more complex patterns that, infinitely often, are bilaterally symmetrical . So it can't build any kind of highway in the usual sense.

"I defy anyone to give a simple classification of the behaviors of all these generalized ants or to predict from their rule-string just what their long-term behavior will be," Nathan declared. "Even if they all start on a clean grid."

Louise looked unhappy. "Yeah, but you haven't proved nobody can do that."

"That's true," I pointed out. "But only slightly more complex transition rules lead to examples such as John Horton Conway's game of Life. Conway proved that in Life there are configurations that form universal Turing machines--programmable computers. Alan M. Turing proved that the long-term behavior of a Turing machine is undecidable -- for example, it is impossible to work out in advance whether or not the program will terminate. Translated into Life terms, that implies that the question 'Does this configuration grow unboundedly?' is formally undecidable. So here's a case where we know the Theory of Everything, and we know a simple question that it is provably impossible to answer on the basis of that theory."

"Exactly," Nathan concurred. "So why do you think a real Theory of Everything, for our universe, can in any meaningful sense be an Ultimate Answer?"

"I dunno," sighed Louise, her faith temporarily shaken. She shook her head, then brightened. "It is a bit of an anty-climax."
 
 

Cohen-Kong Theorem

It is easy to check that the Theory of Everything for Langton's ant is time-reversible--that is, the current pattern and heading uniquely determine the past as well as the future. Any bounded trajectory must eventually repeat the same pattern, position and heading, and by reversibility such a trajectory must be periodic, repeating the same motions indefinitely. Thus, every cell that is visited must be visited infinitely often. The ant's motion is alternately horizontal and vertical, because its direction changes by 90 degrees at each step. Call a cell an H cell if it is entered horizontally and a V cell if it is entered vertically. The H and V cells tile the grid like the black and white squares of a checkerboard.

Select a square M that is visited by the ant and is as far up and to the right as possible, in the sense that the cells immediately above and to the right of it have never been visited. Suppose this is an H cell. Then M must have been entered from the left and exited downward and hence must have been white. But M now turns black, so that on the next visit the ant exits upward, thereby visiting a square that has never been visited. A similar problem arises if M is a V cell. This contradiction proves that no bounded trajectory exists.

SCIENTIFIC AMERICAN July 1994
http://www.fortunecity.com/emachines/e11/86/langton.html