11/2/03: Ordered Solids (Crystals): Crystal Symmetry
2-D Lattices
Bravais lattice: A collection of points in which the neighbourhood
of each point is the same as the neighbourhood of every other point under
some translation.
In a 2-D plane, location of every point in a Bravais lattice can
be described in the form:
R = n1a1 + n2a2, where
n1, n2 are integers a1, a2
are linearly independent vectors called primitive vectors. Choice
of primitive vectors for a lattice is not unique - usually the choice depends
on simplicity or symmetry considerations.
In 2-D there are five Bravais lattices:
-
Square lattice
-
Rectangular lattice
-
Hexagonal lattice
-
Centered Rectangular lattice
-
Oblique lattice: arbitrary choice of primitive vectors with no special
symmetry except inversion symmetry.
If an identical assembly of particles is placed at each site of a Bravais
lattice, we get a lattice with a basis. A basis can destroy the
original symmetry of the underlying Bravais lattice.
Primitive cell: Small basic unit by repeating which over and over one
gets the entire lattice (e.g., a square in a square lattice).
Primitive cells are not unique - but different choices must have the
same area since the volume of a primitive cell is exactly the inverse of
the density of the crystal (Note that in a Bravais lattice the primitive
cell contains exactly one particle and then these cells are put end to
end to fill the crystal).
Primitive cells are free to have any pecuiliar shape as long as they
fit together properly and tile the plane. The different methods by which
one can tile a plane has given rise to the mathematical topic of tilings
or tesselations. For more on tiling of the plane see the slide-show in
Tilings: Plane
and Fancy.
M C Escher (1898-1972), a Dutch artist, used the mathematical
theory of lattices and tiling the plane to create extraordinary works of
art, e.g, The Riders.

Here, a black rider and horse + a white rider and horse forms one primitive
cell and the underlying lattice is a rectangular Bravais lattice.
For more on the life and work of the artist M C Escher:
There are literally thousands of Escher sites on the WWW - just type
Escher in google and see what happens! (Beware: Escher is very addictive
- once you are hooked into it you will be likely to spend hours and hours
poring and pondering over his pictures to the exclusion of other important
matters.) For starters, you can read the brief essay of the mathematical
underpinnings of Escher's work in The
Mathematical Art of M C Escher . There is also a very good
collection of his prints available at Zvi
Har'El's M C Escher Collection where you can click on the thumbnails
to see the large size images.
Rinus Roelofs, a Dutch artist, has taken the concept of lattices as
art-form further along the path shown by Escher. See Roelof's HTML essay
on Not the tiles,
but the joints: A little bridge between M C Escher and Leonardo
da Vinci. Also see the home
page of Roelofs for examples of how mathematics (in particular, group
theory and topology) can inspire art.
As already mentioned , primitive cells are not unique. A particular
choice, built by associating with each lattice point all of space closer
to it than any other lattice point, gives a particular kind of primitive
cell called the Wigner-Seitz cell, which is unique to each lattice.
For more on the Wigner-Seitz cell and its importance in condensed matter
theory see the web-site The
Wigner-Seitz Method for a series of well-illustrated pages on the subject
(Wigner-Seitz cell really becomes important in electronic band theory since
the Brillouin zone is the Wigner-Seitz cell of the reciprocal lattice).
Wigner-Seitz cells are a special case of Voronoi diagrams (i.e., when
the points of interest are arranged in a periodic lattice). For more on
Voronoi diagrams and its multifarious application see the site Geometry
in Action: Voronoi diagrams.
The symmetry operations which leave a crystal invariant can be grouped
under either translational symmetry group or point symmetry group.
The former is the set of all translations which leave the lattice unchanged
while the latter is the set of all rotations/reflections about some axis
for which the lattice is invariant. The space group is the group
of all translations, rotations and reflections that leave a crystal invariant.
A crystal lattice is said to be symmorphic if its space group
is the direct product of the point group and the translation group.
This is not always the case. Sometimes, the combination of a point
group and translational operations might keep the lattice invariant (and
therefore be a member of the space group) although neither of those operations
may be invidually in the space group. Example in 2-D is the existence
of a glide plane, where symmetry is restored by a combination of
reflection AND translation, but by neither of these operations when
they are applied alone. In 3-D, the presence of a screw axis (e.g,
a helical arrangement of atoms) means that the lattice points are symmetric
under a combination of translation and rotation but neither of the operations
individually.
What about tiling of the surface of solid objects ? The surface
is 2-D but the curvature is not flat as in the case of the plane. This
gives rise to several interesting problems.
How to tile the surface of a sphere ? Below is an example of how to
do it using triangles (first suggested by Buckminster Fuller).

Another possibility is to use hexagons and pentagons as in a soccer
ball and the fullerene compound C60. In this context note that
using pentagons alone, one CANNOT tile a flat 2-D plane! A 2-D plane can
only be tiled using objects with 2-fold, 3-fold, 4-fold or 6-fold symmetry
- but not 5-fold symmetry as in the case of a pentagon.
Nature also has to solve the problem of tiling - especially the surfaces
of 3-D objects. A very interesting example is the surface of the spherical
poliovirus.

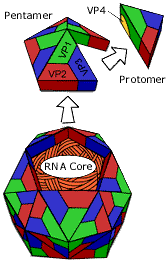
The outer shell (resembling an icosahedron) of the poliovirus is made
out of 60 identical repeating subunits (protomers). Each protomer is made
up of 4 different protein chains VP1, VP2, VP3, VP4. The shell encloses
a core of single stranded RNA, about 7500 nucleotides long.
Most viruses have their outer surface made up of such repeating, geometrically
simple subunits. Why ?
Crick amd Watson suggested that the limited coding capacity of the
tiny virus genome can be best exploited if a virus coat (shell) were composed
of many copies of just a few proteins - and this construction method should
lead to highly symmetrical configurations.
For more details, see J M Hogle, M Chow and D J Filman,
``The structure of poliovirus", Scientific American, March 1987, pp. 28-35.



