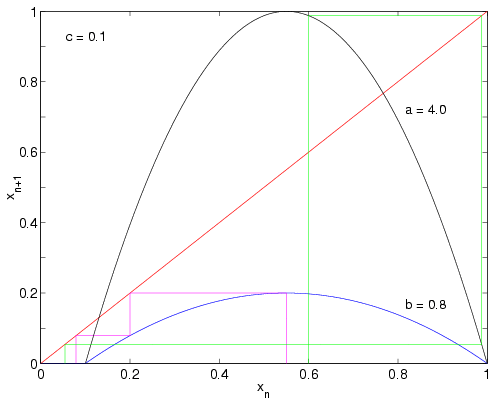
Let us take two maps f1 (source habitat) and f2 (sink habitat) with nonlinearity parameters a = 4 and b = 0.8, respectively.
Allee effect: if the population size falls below a critical level, the population is doomed to extinction (non-sustainability of population below a critical size).

Let us take two maps f1 (source
habitat) and f2 (sink habitat)
with nonlinearity parameters a = 4 and b
= 0.8, respectively.
For f2, the attractor is x=0 - the trapping region makes the convergence to the attractor even faster (at most 3 iterations from any initial value)
For f1, the attractor is chaotic - however, the existence of the trapping region means that the chaos is only transient and eventually the system goes to x = 0.
The time for which the population density is > 0 is called persistence time.
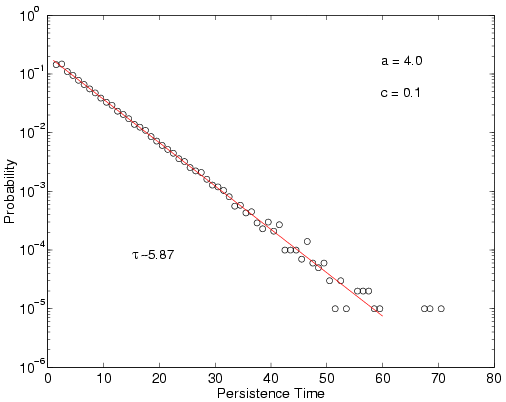
The distribution of persistence times is exponential ~ exp(- t / tau), where tau is the characteristic time (constant for fixed parameters).
Note that, both maps individually have very short persistence times.
Now what happens when we couple
them to each other ?