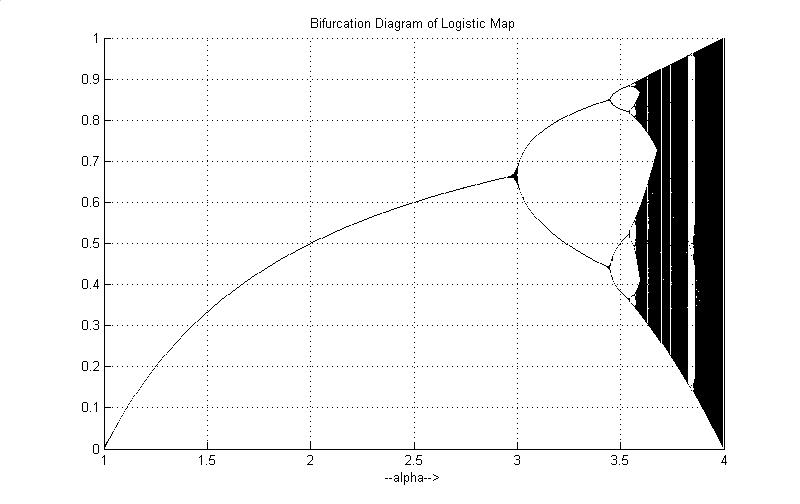
Perhaps the simplest non-linear maps for illustrating chaotic behaviour are the maps of the Logistic Family, having the form:
xn+1 = f(xn) = a xn (1 - xn)
For each value of the parameter a, there is a different map f.
For values of a chosen between 0 and 4, f(x) is a map from the interval [0,1] to itself.
Period-doubling cascade, in which an infinite sequence of attracting 2n-cycles is observed for increasing values of the parameter.