The Logistic Map

Perhaps the simplest non-linear maps for illustrating chaotic behaviour are the maps of the Logistic Family, having the form:

        xn+1 = f(xn) = a xn (1 - xn)

For each value of the parameter a, there is a different map f.

For values of a chosen between 0 and 4, f(x) is a map from the interval [0,1] to itself.

In graphical iteration we draw a `cobweb diagram': we begin at the point x₀ (the initial condition) on the x-axis. Then, from the current point x_n on the orbit, we

• draw a line vertically to the value y_n=f(x_n) - i.e. draw a line vertically to meet the graph of f(x), then
• draw a line horizontally across to meet the diagonal x=y, which the line will intersect at x_n+1=y_n=f(x_n).

The picture illustrates graphical iteration of f with a=2.5 for initial value x₀=0.1.

The applet performs a fixed number of iterations for a chosen initial point (and chosen parameter value), with the final few iterations shown in red to help detect periodic orbits (cycles).

The horizontal slider controls the initial point x₀. The vertical slider controls the parameter value a.

Examples
Shown below are some examples of the behaviour
 

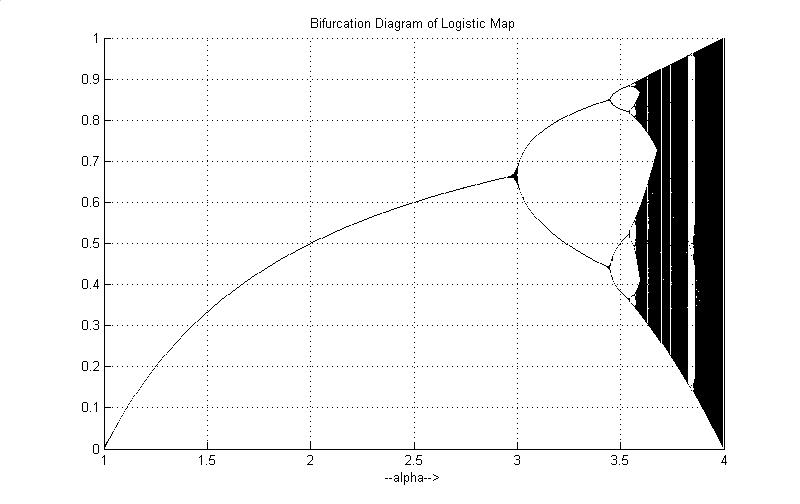
The plots show orbits being attracted to a (stable) 2-cycle, 4-cycle, and 8-cycle (shown, approximately, in red). These three images form part of the period-doubling cascade, in which an infinite sequence of attracting 2ⁿ-cycles is observed for increasing values of the parameter.