Enhanced Persistence of the Coupled System

Let D₁be the migration rate from the source habitat to the sink habitat, and D₂be the migration rate from sink to source.

So the coupled system is described by

x_n+1 = f₁ (x_n - D₁ x_n + D₂ y_n)
y_n+1 = f₂ (y_n - D₂ y_n + D₁ x_n)

where x and y are the source and sink habitat populations respectively.

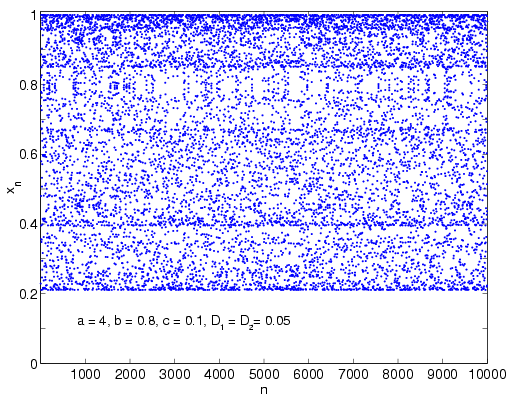
Time series of the source habitat population when the two habitats are coupled to each other.

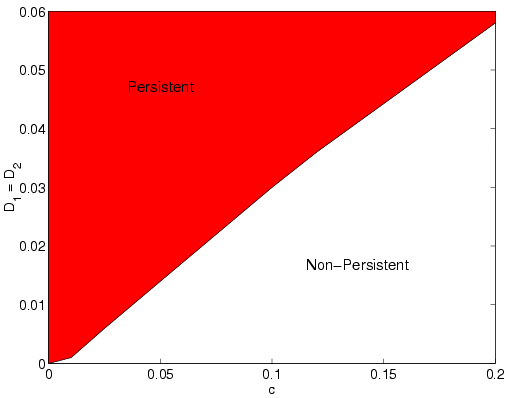
The persistence time of the coupled system becomes infinitely long for a large range of values of the parameters c, D₁ and D₂.

What is the mechanism for this enhanced persistence ?

There are other examples of combination of losing games giving a resultant winning game - notably the Parrondo games.