Symmetric Functions: Problem Set 9
- Show that the definitions of the induced representation IndHG(W)
(given in lecture) make it a representation of G.
- Prove Frobenius reciprocity; given a H-map f : W → U, there is a
unique G-map
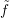 such that
such that 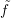 ∘ i = f where i is the natural inclusion
from W → IndHG(W).
∘ i = f where i is the natural inclusion
from W → IndHG(W).
- For each irrep W of S3, compute the decomposition of IndS3S4W into
irreps of S4, using the inner product version of Frobenius reciprocity.
- If X is a transitive G-set and H is the stabilizer of an element of
X, prove that IndHG(W) is isomorphic to ℂ[X], where W is the one
dimensional trivial representation of H.
- Let W be an irrep of H. Prove that ⟨IndHG(W),IndHG(W)⟩≤ [G :
H].
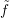 such that
such that 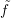 ∘ i = f where i is the natural inclusion
from W → IndHG(W).
∘ i = f where i is the natural inclusion
from W → IndHG(W).
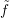 such that
such that 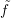 ∘ i = f where i is the natural inclusion
from W → IndHG(W).
∘ i = f where i is the natural inclusion
from W → IndHG(W).