Symmetric Functions: Problem Set 7
- Let {uλ},{u′λ} (and similarly {vλ},{v′λ}) be a pair of dual bases of
Λ with respect to the form ⟨,⟩. If
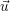 =
= 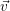 A, prove that
A, prove that 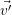 =
= 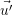 A′.
A′.
- Let λ,μ ∈ Par(d). Prove that if λ is a refinement of μ, then λ occurs
after μ in reverse lexicographic order. Is it true that μ dominates λ ?
- Prove Pieri’s rule (in the ring of symmetric functions in n variables,
for large n): sλhk = ∑
μ∈λ⊗ksμ where λ ⊗ k is the set of partitions
obtained by adding k boxes to the diagram of λ, no two in the same
column. Deduce that the same equation holds in the ring Λ.
- Let
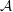 denote the space of alternating polynomials in n variables. Show
that (i) The aγ for γ ∈ D(n) span
denote the space of alternating polynomials in n variables. Show
that (i) The aγ for γ ∈ D(n) span 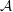 , (ii) multiplication by aδ defines
an isomorphism of vector spaces Λn →
, (ii) multiplication by aδ defines
an isomorphism of vector spaces Λn →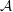 . Thus,
. Thus, 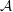 is a free Λn-module
generated by aδ.
is a free Λn-module
generated by aδ.
- Let δ = (n-1,n-2,
 ,0). Show that sδ = ∏
1≤i<j≤n(xi+xj) in the
ring Λn. Compute skδ for all k ≥ 1.
,0). Show that sδ = ∏
1≤i<j≤n(xi+xj) in the
ring Λn. Compute skδ for all k ≥ 1.
- Prove the identities:
| fλ | = ∑
λ∈μ⊗1fμ | (1)
|
| (1 + |λ|)fλ | = ∑
μ∈λ⊗1fμ | (2) |
where fλ is the number of standard Young tableaux of shape λ.
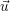 =
= 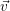 A, prove that
A, prove that 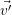 =
= 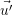 A′.
A′.
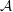 denote the space of alternating polynomials in n variables. Show
that (i) The aγ for γ ∈ D(n) span
denote the space of alternating polynomials in n variables. Show
that (i) The aγ for γ ∈ D(n) span 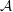 , (ii) multiplication by aδ defines
an isomorphism of vector spaces Λn →
, (ii) multiplication by aδ defines
an isomorphism of vector spaces Λn →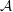 . Thus,
. Thus, 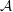 is a free Λn-module
generated by aδ.
is a free Λn-module
generated by aδ.
 ,0). Show that sδ = ∏
1≤i<j≤n(xi+xj) in the
ring Λn. Compute skδ for all k ≥ 1.
,0). Show that sδ = ∏
1≤i<j≤n(xi+xj) in the
ring Λn. Compute skδ for all k ≥ 1.