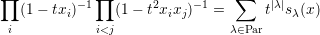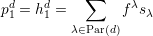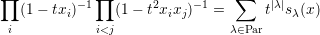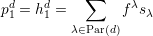Symmetric Functions: Problem Set 6
  1. Let b ∈{m,h,p,s}. Let n ≥ 1. Prove that {bλ : ℓ(λ) ≤ n} is a basis of Λn.
  2. Let n ≥ 1. Prove that {eλ′ : ℓ(λ) ≤ n} is a basis of Λn.
  3. What is the corresponding statement for the {fλ} (the forgotten symmetric functions)?
  4. Prove that ω is an isometry (Hint: compute using s).
  5. Using the symmetry property of the RSK algorithm, prove that
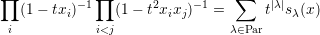
    ∏ ∏ ∑ (1- txi)-1 (1- t2xixj)-1 = t|λ|sλ(x) i i<j λ∈Par

  6. Prove that the matrix of ω in the m-basis is triangular. Do the same for the bases e,h,f.
  7. Prove that
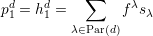
    pd= hd= ∑ f λs 1 1 λ λ∈Par(d)

    where fλ is the number of standard Young tableaux of shape λ.

  8. Use the above to show that fλ is the dimension of V (λ).