Symmetric Functions: Problem Set 5
  1. Compute the action of the involution ω on each of the following: mλ,eλ,hλ,fλ,pλ,sλ.
  2. Show by comparing the actions of ω on pλ and sλ that the number of even partitions of d (those for which the permutation of that cycle type is even) minus the number of odd partitions of d is equal to the number of self conjugate partitions of d.
  3. Show that if λ = 1m12m2⋅⋅⋅ is a partition of d, the number of elements in Sd of cycle type λ is d!∕zλ where zλ = 1m1m1!2m2m2!⋅⋅⋅.
  4. Prove that
    ∏ i,j(1 - txiyj)-1 = ∑ λ∈Part|λ|s λ(x)sλ(y) (1)
    = ∑ λ∈Part|λ|z λ-1p λ(x)pλ(y) (2)
  5. Prove that
    ∏ i,j(1 + txiyj) = ∑ λ∈Part|λ|s λ(x)sλ′(y) (3)
    = ∑ λ∈Part|λ|z λ-1ϵ λpλ(x)pλ(y) (4)
    where ϵλ is the sign of the permutation wλ of cycle type λ.
  6. Let {uλ : λ ∈ Par(d)} and {vλ : λ ∈ Par(d)} be bases of Λd for each d ≥ 1. Let
    ⃗u = ⃗sA and ⃗v = ⃗sB

    (there is one such A,B for each d). Suppose AB′ = I for each d ≥ 1, show that:

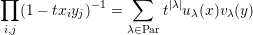
    ∏ ∑ (1 - txiyj)- 1 = t|λ|uλ(x)vλ(y) i,j λ∈Par