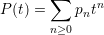
Show the following:
| P(t) | = ∑
i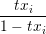 = t = t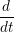 ∑
i log(1 - txi)-1 ∑
i log(1 - txi)-1 | (1) |
| P(t) | = t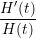 | (2) |
| P(-t) | = -t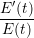 | (3) |
| ∑ r=1np rhn-r | = nhn(n ≥ 1) | (4) |
| ∑ r=1n(-1)r-1p ren-r | = nhn(n ≥ 1) | (5) |
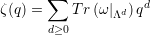
Prove that ζ(q) = 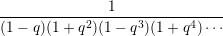 .
.

prove that Tr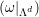 equals the number of self conjugate partitions of
d.
equals the number of self conjugate partitions of
d.