Symmetric Functions: Problem Set 3
- Prove that the map ω : ei
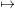 hi defined in lecture is indeed an involution
(we only did this by example).
hi defined in lecture is indeed an involution
(we only did this by example).
- Define fλ := ω(mλ). The fλ are called the forgotten symmetric
functions. Show that they form a basis of Λ. Compute fλ for |λ| =
1,2,3.
- Compute the change of basis matrix when eλ is written in terms of
the fμ.
- Let xi = 1 for 1 ≤ i ≤ n and xi = 0 for i > n. Show that under this
substitution, er =
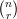 . Find the values of hr and mλ for r ≥ 1 and
λ ∈ Par.
. Find the values of hr and mλ for r ≥ 1 and
λ ∈ Par.
- Let us substitute xi = 1∕n for 1 ≤ i ≤ n and xi = 0 otherwise. Now
take the limit as n →∞. Compute the values of er,hr and mλ in this
limit.
- Prove that:
| en | = det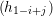 1≤i,j≤n 1≤i,j≤n | |
|
| hn | = det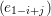 1≤i,j≤n 1≤i,j≤n | | |
- If hn = n for each n ≥ 1 (recall that the hn are algebraically independent
generators, and one can assign any value to them), the sequence (en)n≥1, is
periodic with period 3.
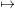 hi defined in lecture is indeed an involution
(we only did this by example).
hi defined in lecture is indeed an involution
(we only did this by example).
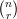 . Find the values of hr and mλ for r ≥ 1 and
λ ∈ Par.
. Find the values of hr and mλ for r ≥ 1 and
λ ∈ Par.
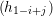 1≤i,j≤n
1≤i,j≤n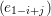 1≤i,j≤n
1≤i,j≤n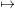 hi defined in lecture is indeed an involution
(we only did this by example).
hi defined in lecture is indeed an involution
(we only did this by example).
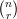 . Find the values of hr and mλ for r ≥ 1 and
λ ∈ Par.
. Find the values of hr and mλ for r ≥ 1 and
λ ∈ Par.
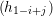 1≤i,j≤n
1≤i,j≤n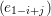 1≤i,j≤n
1≤i,j≤n