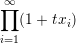

 ,1)(x). For
a partition λ = (λ1,λ2,
,1)(x). For
a partition λ = (λ1,λ2, ,λp) of d, define:
,λp) of d, define:
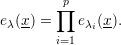
Write eλ(x) as a linear combination of the basis {mμ(x) : μ ∈ Par(d)} for d = 1,2,3,4 and each choice of λ.
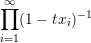
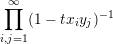
 ,λp) of d, define:
,λp) of d, define:
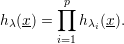
Write hλ(x) as a linear combination of the basis {mμ(x) : μ ∈ Par(d)} for d = 1,2,3,4 and each choice of λ.
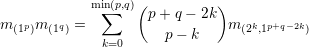
 , i.e,
there is a polynomial fλ ∈ k[u1,u2,
, i.e,
there is a polynomial fλ ∈ k[u1,u2, ] such that mλ = f(e1,e2,
] such that mλ = f(e1,e2, ).
).