Symmetric Functions: Problem Set 11
  1. Complete the proof of the hook-content formula by simplifying the product obtained in class into the required form.
  2. Prove that the skew Schur functions are symmetric functions by adapting the argument used for Schur functions (free and paired occurrences of i, i + 1 etc).
  3. Prove that:
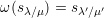
    ω (sλ∕μ) = sλ′∕μ′

  4. Let μ,ν be partitions of d; thus V (μ), V (ν) and V (μ) ⊗ V (ν) are all representations of Sd. Define:
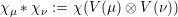
    χμ *χ ν := χ(V (μ)⊗ V (ν))

    We have

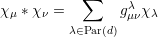
    ∑ λ χ μ * χν = gμνχλ λ∈Par(d)

    The gμνλ are nonnegative integers, called the Kronecker coefficients. Prove that gμνλ is symmetric in μ,ν,λ.

  5. Let x,y respectively denote the infinite list of variables x1,x2,⋅⋅⋅ and y1,y2,⋅⋅⋅. Prove that:
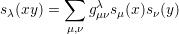
    ∑ sλ(xy) = gλμνsμ(x)sν(y) μ,ν

    where xy denotes the list of variables xiyj for (i,j) ∈ ℕ × ℕ. Hint: Expand in terms of power sums first.

  6. Prove :
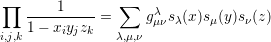
    ∏ ----1----- ∑ λ 1 - xiyjzk = gμνsλ(x )sμ(y)sν(z) i,j,k λ,μ,ν

  7. Define
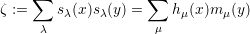
    ∑ ∑ ζ := sλ(x)sλ(y) = hμ(x)m μ(y) λ μ

    each side being equal to ∏ i,j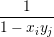---1---- 1 - xiyj.

    1. Verify that ζ = ∑ αyαhα(x) where the sum runs over all possible multi-indices α.
    2. This identity holds if we restrict x and y to finite lists of variables x1,x2,⋅⋅⋅,xn and y1,y2,⋅⋅⋅,yn. The sums on both sides then run over partitions with at most n parts (since sλ = 0 = mμ if λ,μ have more than n parts). Show that sλ(x) is the coefficient of yλ+δ in ζaδ(y).
    3. Recall aδ = ∑ w∈Snsgnwywδ. Use this to show that:
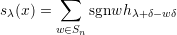
      ∑ sλ(x) = sgnwh λ+δ-wδ w ∈Sn
      		(1)

      where hi is taken to be zero for i < 0.

    4. Prove that the above expression is nothing but the determinant:
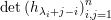
      det(h )n λi+j-i i,j=1

      This identity is called the Jacobi-Trudi identity.

    5. Derive an analogous expression for sλ in terms of the ek.
    6. Use equation (1) to give an expression for the entries Kλμ-1 of the inverse Kostka matrix.