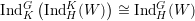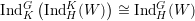Symmetric Functions: Problem Set 10
  1. Let G be the dihedral group with 2n elements and H its subgroup isomorphic to the cyclic group of order n. What are the irreducible representations of H ? What are the dimensions of the irreducible representations of G ? For which irreps W of H is IndHGW an irrep of G ?
  2. Let G be the cyclic group Cn and let H be its cyclic subgroup isomorphic to Cd (where d|n). For each irrep W of H, describe the decomposition into G-irreps of IndHGW.
  3. Let H ⊂ K ⊂ G, and let W be a representation of H. Prove :
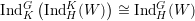
    G ( K ) ~ G IndK IndH (W ) = IndH (W )

    (use the universal property of the induced representation)

  4. Prove that the multiplication defined on the ring R (the span of class functions of Sd for all d) is commutative and associative.
  5. Let V be a finite dimensional representation of Sd, and let χ denote its character. Prove that ch(χ) is Schur positive, i.e., it can be written as a ℤ+ linear combination of Schur functions.
  6. Prove that the product of any two Schur functions is Schur positive. The non-negative integers cλμν in:
    ∑ sλsμ = cνλμsν ν

    are called Littlewood-Richardson coefficients.