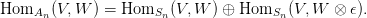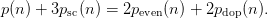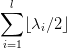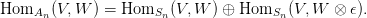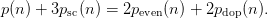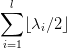REPRESENTATION THEORY OF FINITE GROUPS

PROBLEMS SET 8

Date: 20th June 2017.

  1. Show that the number of inversions in the transposition (i,j) is 2(j - 1 - 1) + 1, so that ϵ((i,j)) = -1.
  2. Let V and W be representations of Sn. Show that
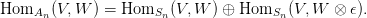
    HomAn (V,W ) = HomSn (V, W ) ⊕ HomSn (V, W ⊗ ϵ).

  3. Let X be a set with an action of Sn. Given x ∈ X, show that the Sn-orbit of x is a union of two orbits for the action of An if and only if StabSnx ⊂ An.
  4. How many conjugacy classes does A5 have? What are their cardinalities?
  5. What must be the dimensions of the irreducible representations of A5?
  6. Let p(n) denote the number of partitions of n. Let peven(n) denote the number of partitions of n with an even number of even parts. Let pdop(n) denote the number of partitions of n with distinct odd parts. Let psc(n) denote the number of self-conjugate partitions of n. Prove that:
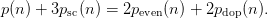
    p(n) + 3psc(n) = 2peven(n) + 2pdop(n).

  7. For an odd integer n > 2, show that a n-cycle is conjugate to its inverse in An if and only if ⌊n∕2⌋ is even.
  8. An element of An with cycle type λ, where λ has distinct odd parts is conjugate to its inverse if and only if
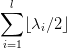
    ∑l ⌊λi∕2⌋ i=1

    is even.