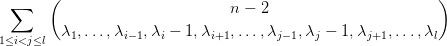
is even (this is a multinomial coefficient of n - 2. In the lower row, the ith and jth parts of λ are reduced by 1).
Date: 19th June 2017.
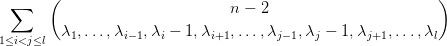
is even (this is a multinomial coefficient of n - 2. In the lower row, the ith and jth parts of λ are reduced by 1).