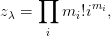
where for each i = 1, 2, 3,…, mi is the number of times i occurs in the partition λ. Note that this means that the number of permutations with cycle type λ is n!∕zλ
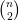 - k
inversions.
- k
inversions.
Date: 16th June 2017.
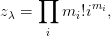
where for each i = 1, 2, 3,…, mi is the number of times i occurs in the partition λ. Note that this means that the number of permutations with cycle type λ is n!∕zλ
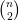 - k
inversions.
- k
inversions.