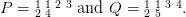
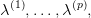
where p is the number of partitions of n. Define p × p matrices
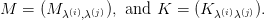
Compute M and K for n = 2, 3, 4. Verify that M = K′K.
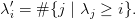
Show that conjugation reverses dominance:

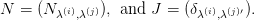
Here δ is the Kronecker delta symbol. For n = 2, 3, 4, verify that N = K′JK.
Date: 15th June 2017.
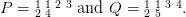
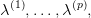
where p is the number of partitions of n. Define p × p matrices
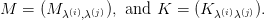
Compute M and K for n = 2, 3, 4. Verify that M = K′K.
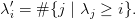
Show that conjugation reverses dominance:

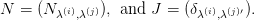
Here δ is the Kronecker delta symbol. For n = 2, 3, 4, verify that N = K′JK.