REPRESENTATION THEORY OF FINITE GROUPS

PROBLEMS SET 3

Date: 14th June 2017.

  1. Let A be an integer matrix with RSK(A) = (P,Q). Describe RSK(mA) for any positive integer m.
  2. Given non-negative integers a and b, describe the shape of the tableaux in RSK(
    0a
    b0
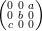    ). What about the tableaux corresponding to (0 0 a) 0c b 0 00?
  3. Given a subset S ⊂{1,…,n} of size k, where k ≤ n∕2, let AS denote the n × 2 matrix with entries defined by
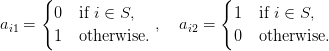
    { { a = 0 if i ∈ S, , a = 1 if i ∈ S, i1 1 otherwise. i2 0 otherwise.

    Note that every n × 2 matrix with row sums all one, and column sums (n - k,k) is of the form AS for some such S. Supose that RSK(AS) = (PS,QS). Show that ϕn,k : S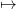↦→QS is a bijection from the set of subsets of {1,…,n} of size k onto the set of all standard Young tableaux of shape (n - l,l) for some 0 ≤ l ≤ k. This gives a bijective proof of the identity

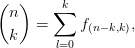
    ( ) ∑k n = f(n-k,k), k l=0

    for k ≤ n∕2 (see Problems Set 1, Ex. 3(b)).

  4. Enumerate the six subsets of size 2 in {1, 2, 3, 4}. Compute ϕ4,2(S) for each of these subsets S.
  5. Give a direct construction of the bijection ϕn,k without using the RSK correspondence.