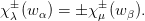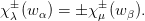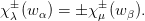REPRESENTATION THEORY OF FINITE GROUPS

PROBLEMS SET 11

Date: 23rd June 2017.

  1. Compute χ(3,2,1)(2, 2, 2).
  2. For each positive integer n, let λ = (n,…,n) denote the partition of n2 with all parts equal to n. Show that
    χλ (2n - 1,2n - 3,...,3,1) = (- 1)⌊n∕2⌋.

  3. Let gλ denote the number of standard Young tableaux of shape λ with 2 occuring in the first column. For any partition λ of n ≥ 2, show that the character value χλ((1, 2)) at a 2-cycle fλ - 2gλ.
  4. Show that det ∘ρλ : Sn → C* is the sign chatacter of S n if and only if gλ is odd. Such partitions are called chiral partitions1 . [Hint: what are the eigenvalues of ρλ(s1)?]
  5. Show that, if λ is a self-conjugate partition of n, then either a box can be added to the Young diagram of λ to obtain the Young diagram of a self-conjugate partition of n + 1, or a box can be removed from the Young diagram of λ to obtain the Young diagram of a self-conjugate partition of n + 1.
  6. We say that (λ,μ) is a self-conjugate cover if both λ and μ are self-conjugate, and the Young diagram of λ is obtained from the Young diagram of μ by removing one box. List all the self-conjugate covers involving partitions up to size eight.
  7. If (λ,μ) is a self-conjugate cover, λ = ϕ(α), and μ = ϕ(β) for some partitions α and β with distinct odd parts, then show that
    χ ±(w ) = ±χ ±(w ). λ α μ β