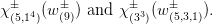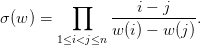
Show that σ(w) coincides with the sign character value ϵ(w).
| χ(5,14)(w(9)) | = 1, | ||
| χ(5,14)(w(5,3,1)) | = 0, | ||
| χ(33)(w(9)) | = 0, and | ||
| χ(33)(w(5,3,1)) = -1, |
Date: 22nd June 2017.
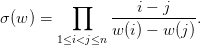
Show that σ(w) coincides with the sign character value ϵ(w).
| χ(5,14)(w(9)) | = 1, | ||
| χ(5,14)(w(5,3,1)) | = 0, | ||
| χ(33)(w(9)) | = 0, and | ||
| χ(33)(w(5,3,1)) = -1, |