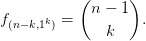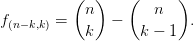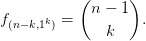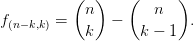REPRESENTATION THEORY OF FINITE GROUPS

PROBLEMS SET

Date: July 2, 2017.

  1. Let p(n) denote the number of integer partitions of n. Prove that p(n) ≤ p(n - 1) + p(n - 2) for each n ≥ 2. Conclude that p(n) grows faster than Fibonacci numbers.
  2. Suppose that λ = (n - l,l) and μ = (n - m,m), with 0 ≤ l,m ≤ n∕2. Show that there exists a unique SSYT of shape μ and type λ if and only if m ≤ l. If m > l, then there is no such SSYT.
  3. For an integer partition λ, let fλ denote the number of standard Young tableaux of shape λ. Let n be any positive integer.
    1. For each 0 ≤ k < n, show that
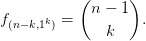
      (n - 1 ) f(n-k,1k) = . k

    2. For each 0 ≤ k ≤ n∕2, show that
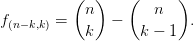
      ( ) ( ) n n f(n- k,k) = k - k - 1 .

  4. Find the least value of n for which the reverse dominance order on the set of partitions of n is not a linear order (i.e., there exist partitions λ and μ of n such that neither λ ≤ μ, nor μ ≤ λ.
  5. Let λ be a hook, i.e., λ = (m, 1k) for some positive integer m and some nonnegative integer k. Which are the partitions μ of m + k that satisfy μ ≤ λ.
  6. Show that, if μ ≤ λ in the reverse dominance order, then the number of parts of μ is at most the number of parts of λ.
  7. Exhibit a SSYT of shape (5, 2, 2) and (3, 3, 3). What is the Kostka number K(5,2,2),(3,3,3)?
  8. Determine the number of 3 × 3 matrices with nonnegative integer entries whose rows and columns all add up to 3 (this is the number M(3,3,3),(3,3,3)).